结构光三维立体成像
罗汉杰,CVTE中央研究院
Slide
Introduction
我们生活在三维的空间中,然而,传统的摄像机和图像传感器只能获取二维的图像,缺乏深度的信息,这对感知和了解真实的物体造成了极大的限制。而最近几十年,随着高清,高速图像传感器和计算能力的不断发展,三维表面成像技术在研究,工程和商业上取得了显著的成果。特别是结构光三维表面成像技术,已经运用到各个地方中,从MEMS组件的表面测量到大面积平面厚度测量(2.5m×0.45m)1。结构光的显著的优点是能够通过非接触的方式,建立高分辨率,全幅的物体三维模型,合适于运用在对成像面积,精度有一定要求的应用中。
一般的3D影像技术中,可以用一个坐标系为\(\text{(x,y,z)}\)的空间中描述三维物体的属性。而3D表面成像技术,是专门用来测量物体表面的。测量的结果可以用一个以\(\lbrace z=h(x,y),x=1,2,...,L,y=1,2,...,M \rbrace\)为形式的矩阵来描述。\((x,y)\)为笛卡尔坐标系中的点坐标,\(z\)为该点的高度。
本文主要讲述构光三维表面成像技术,特别是相位测量轮廓术(Phase measuring profilometry, PMP)的原理和实现方式。
Structured-light 3D Surface Imaging System
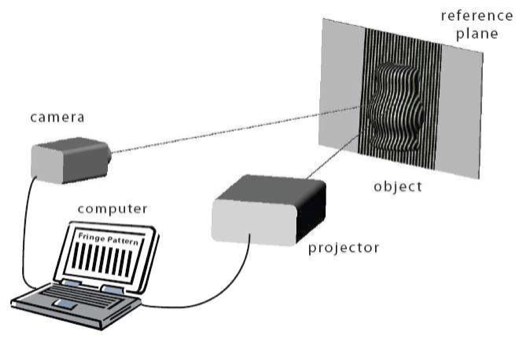
下图2描述了一个经典的结构光三维表面成像系统。它包括一个投影模块(Projector),图像获取模块(Camera)和处理模块(Computer)。通过对目标物体表面主动投影一个有一定结构的二维纹理图像(如图所示的黑白光栅图),获取其随着物体表面高度变化而变形的二维纹理图,然后利用处理模块根据算法计算出物体表面三维几何结构。
结构光三维成像技术根据实现方式的不同能分为很多类。根据拍摄次数的不同能分为多次拍摄(multiple-shot)和单次拍摄(single-shot)两个大类3。如果物体保持静止,并且应用对于获取时间没有严格要求的情况下,多次拍摄的方法一般能产生更可靠和更准确的结果。然而,如果物体是运动的话,则可以利用单次拍摄的方法获取物体在某个时间点的三维表面图像。本文中,我们主要讨论多次拍摄技术中的相位测量轮廓术(phase-measuring profilometry,PMP,也称作Fringe projection profilometry。Phase shift method 属于PMP的一种)。
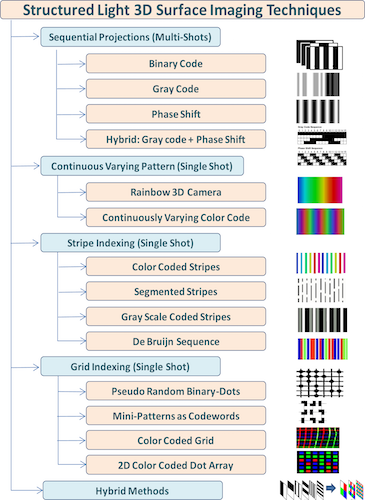
相对于Binary code和Gray code等编码结构光法,PMP不需要复杂的编码,并且算法可以根据每一个像素点的信息计算出高度数值,从而实现全幅高精度测量。在相位法中,通常包含以下步骤4:
- 投影一个结构纹理图像(通常是一个正弦光栅图案)到待测物体表面。
- 记录被物体高度所相位调制的光栅图像。
- 利用光栅分析技术提取相位。
- 使用合适的相位展开算法,获得与物体高度等比例变化的连续相位分布。
- 标定系统,将展开了的相位分布映射到真实世界的三维坐标系中。
在每一个步骤中,都存在多种的变体。而根据相位提取方法的不同,相位法可以分为Phase shift profilometry (PSP,也称作Phase stepping profilometry),Fourier transform profilometry (FTP),Wavelet transform profilometry (WTP),Spatial filtering profilometry (SFP)等几个大类。本文主要讨论PMP中的Phase shift profilometry。
Phase Measuring Profilometry
Model
PMP方法的光学几何结构如下图5所示。投影模块产生的正弦光栅图像投影到放在参考平面(Reference plane)的物体表面上,所折射的光被图像获取模块(Camera)捕获。由于所投影的正弦图在列方向都是以相同模式改变的,所以物体的轮廓能够通过每一行的计算结果组建起来。
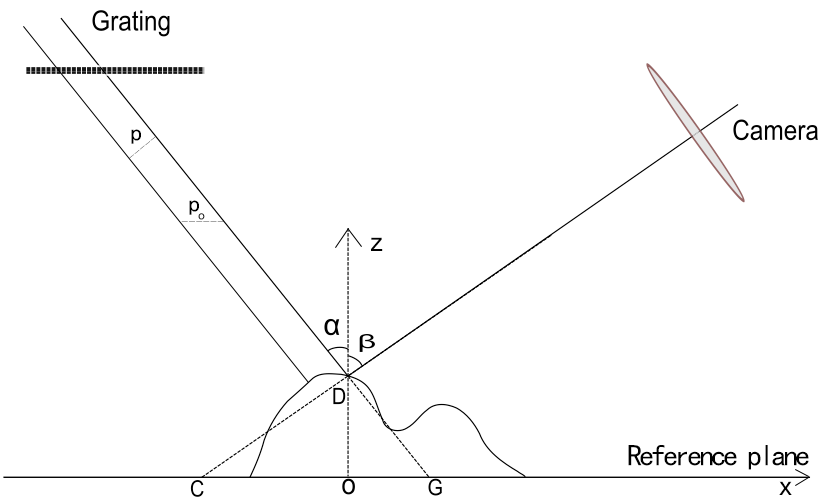
在上图的例子中,我们假设O点为光轴跟参考平面的交点,O点被用作坐标原点并且相位为0。投影到参考平面上的正弦光栅图周期为\(p_{o}\),原始正弦光栅图周期为\(p\),\(p=p_{o}\cdot\cos\alpha\)。Camera中的传感器接收到在物体表面D点反射的光线;如果没有物体的话,传感器中的同一位置将会接收到在参考平面上的C点所反射的光线。相应地,物体表面D点折射的光线,跟没有物体的情况下水平面上G点折射的光线相同。所以投影图像在D点的相位相跟在G点的相位相等,有:
\[\begin{align} \phi_{D}=\phi_{G} \end{align}\]
\(\phi_{C}=2\pi OC/p_{o}\)为投影图像在C点的相位值。点D跟点C的相位差为:
\[\begin{align} \Delta\phi_{CD} &= \phi_{C}-\phi_{D}=\phi_{C}-\phi_{G} \label{eq:2.2} \newline &= 2\pi OC/p_{o}-2\pi OG/p_{o}=2\pi CG/p_{o} \notag \end{align}\]
根据几何关系,有:
\[\begin{align} CG=OD(\tan\alpha+\tan\beta)\label{eq:2.3} \end{align}\]
根据公式\(\ref{eq:2.2}\),\(\ref{eq:2.3}\),有:
\[\begin{align} OD=\frac{\Delta\phi_{CD}\cdot p_{o}}{2\pi(\tan\alpha+\tan\beta)}\label{eq:2.4} \end{align}\]
OD即为物体在点O的高。上式的一般式为:
\[\begin{align} h(x,y)=\frac{[\phi_{o}(x,y)-\phi_{r}(x,y)]\cdot p_{o}}{2\pi(\tan\alpha+\tan\beta)}\label{eq:2.13} \end{align}\]
\(\phi_{o}(x,y)\)为在点\((x,y)\)中的相位,\(\phi_{r}(x,y)\)为在相应点中参考平面上的相位。在实际系统中,由于\(\beta\)的值接近于\(0^{\circ}\),所以公式\(\ref{eq:2.13}\)也可以写成以下近似公式6:
\[\begin{align} h(x,y)\approx\frac{[\phi_{o}(x,y)-\phi_{r}(x,y)]\cdot p_{o}}{2\pi\tan\alpha}\label{eq:2.5} \end{align}\]
从公式\(\ref{eq:2.5}\)可以看出,物体的高度信息可以通过提取投影在物体上的正弦图像相位值和投影在相应位置的水平面上的相位值计算所得。下一小节将介绍如何使用相移法(Phase shift profilometry)进行相位提取。
Phase Shift Profilometry
当在光照稳定,Camera是线性的情况下,所拍摄的图像中某点\((x,y)\)的光照强度\(I(x,y)\)能够表达为以下公式7:
\[\begin{align} I(x,y)=B(x,y)+C(x,y)\cos\phi(x,y)\label{eq:2.6} \end{align}\]
\(B(x,y)\)为背景光强,\(C(x,y)\)为正弦光栅的幅度值,\(\phi(x,y)\)为受物体高度调制后的相位值。\(I(x,y)\)可以通过Camera获得,为了消掉公式中的\(B(x,y)\)和\(C(x,y)\)而得到\(\phi(x,y)\),我们使用一种称作相移法的相位提取算法。在相移法中,相位将移动\(k(k\geq3)\)次,每次移动相等的值\(\theta_{k}\),\(\theta_{k}<2\pi\)。则公式\(\ref{eq:2.6}\)可以写成:
\[\begin{align} I_{k}(x,y) &= B(x,y)+C(x,y)\cos[\phi(x,y)+\theta_{k}] \label{eq:2.7} \newline &= B(x,y)+C(x,y)[\cos\phi(x,y)\cos{\theta_{k}}+\sin\phi(x,y)\sin\theta_{k}] \notag \end{align}\]
一般我们获取4张图片8。令\(\theta_{k}=(k-1)\pi/2\),\(k=\lbrace 1,2,3,4 \rbrace\),代入公式\(\ref{eq:2.7}\),可以得到:
\[\begin{align} B(x,y) & =\frac{1}{4}[I_{1}(x,y)+I_{2}(x,y)+I_{3}(x,y)+I_{4}(x,y)]\label{eq:2.8}\newline \cos\phi(x,y) & =\frac{I_{1}(x,y)-I_{3}(x,y)}{2C(x,y)}\label{eq:2.9}\newline \sin\phi(x,y) & =\frac{I_{4}(x,y)-I_{2}(x,y)}{2C(x,y)}\label{eq:2.10} \end{align}\]
从公式\(\ref{eq:2.9}\),\(\ref{eq:2.10}\)可以得到:
\[\begin{align} \tan\phi(x,y)=\frac{I_{4}(x,y)-I_{2}(x,y)}{I_{1}(x,y)-I_{3}(x,y)}\label{eq:2.11} \end{align}\]
因此我们得到相位值:
\[\begin{align} \phi(x,y)=\arctan\left(\frac{I_{4}(x,y)-I_{2}(x,y)}{I_{1}(x,y)-I_{3}(x,y)}\right) , \phi(x,y)\in[-\pi,\pi)\label{eq:2.12} \end{align}\]
然后物体表面高度可以根据公式\(\ref{eq:2.5}\)得出。
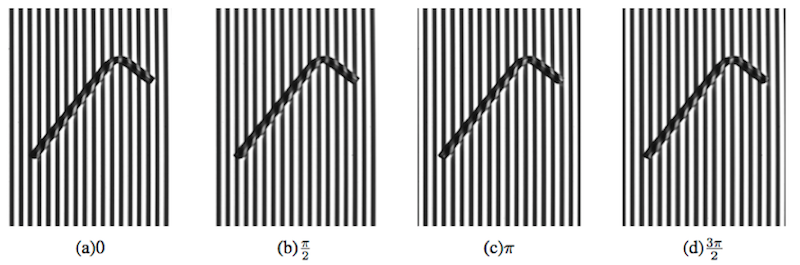
相移法由于利用多幅图像的光强信息计算得每一点的相位,具有一定的抗噪能力。但在采样的过程中,要求物体保持静止,所以不适合于动态测量。下图显示当\(k=4\)时,使用相移法将4张不同相位的正弦光栅图像投影到物体表面时的照片。可以看出,投影的光栅图像每次移动四分之一个周期。
Phase Unwrapping
我们通过公式\(\ref{eq:2.12}\)计算获得相位值\(\phi(x,y)\)。然后在反正切计算中,所得的结果总是在\([−π, π)\)之间,而真正的相位即绝对相位应该是连续的,所以我们在相位展开时,需要作相应处理。
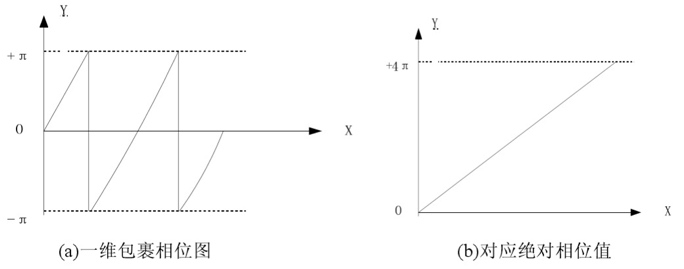
假定\(\phi^{wrap}\)表示被包裹的相位值,那么对相邻的两个相位\(\phi _1^{wrap}\),\(\phi _2^{wrap}\)进行展开运算\(U(\phi _2^{wrap}, \phi _1^{wrap})\):
\[\begin{align} U(\phi _2^{wrap}, \phi _1^{wrap}) = \phi _2^{wrap} - 2\pi R[(\phi _2^{wrap} - \phi _1^{wrap}) / 2\pi]\label{eq:2.14} \end{align}\]
\(R(\cdot)\)表示四舍五入到最接近的整数。所以,对于\(\phi _s^{wrap}\)的相位展开操作为:
\[\begin{align} \phi _{s}^{unwrap} = \sum _{t = 1}^s U( \phi _{t}^{wrap} , \phi _{t-1}^{wrap}) \label{eq:2.15} \end{align}\]
我们这里仅仅介绍了一种简单的相位展开操作,它对于相位展开时的路径十分敏感,错误的路径会导致错误的展开结果(如下图所示)。
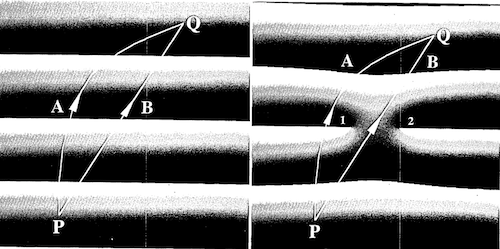
Appendix
Generation of Sinusoidal Pattern
相位测量轮廓术需要将具有不同相位的正弦光栅图案投影到物体表面上。传统方法采用两束激光,利用干涉原理生成正弦光栅图,相位的移动利用压电晶体实现9。然而激光干涉产生的斑点噪音会影响光栅图像的光强分布。另一方面,由于压电晶体的非线性属性,使得相位移动的产生误差。也有一些相位移动是通过步进电机位移平台实现的10。但系统的精度也难免受到平台移动时的震动而影响。
液晶投影仪能够利用个人电脑控制投影的图像。通过投影软件生成正弦光栅图像,它提供了一种高效的结构光投影方案。我们假设液晶投影仪的分辨率为\(R\times C\)。对于生成的正弦光栅图中的每一列\(c\),\(c=0,1,2,...,C-1\),有:
\[\begin{align} F_{n}(r,c) & =\lbrace 1+\sin\lbrace \frac{2\pi}{p}[r+(k-1)\delta] \rbrace \rbrace \cdot127.5\newline r & =0,1,2,...,R-1 \notag \label{eq:3.1} \end{align}\]
\(F_{n}(r,c)\)是相移\(k\)步后的光栅图中\((r,c)\)位置的像素值,在我们的例子中,\(k=\lbrace 1,2,3,4 \rbrace\);\(p\)是以像素为单位的光栅周期;\(\delta\)为相位移动增量。当\(|k|=4\)时,相位的增量为\(\pi/2\),所以相应地,\(\delta=p/4\)。下图显示了使用软件生成的正弦光栅图,每一张图都比上一张图往右移动了四分之一个周期。

S. S. Gorthi and P. Rastogi, “Fringe projection techniques: whither we are?,” Optics and Lasers in Engineering, vol. 48, no. IMAC-REVIEW-2009-001, pp. 133–140, 2010.↩︎
S. S. Gorthi and P. Rastogi, “Fringe projection techniques: whither we are?,” Optics and Lasers in Engineering, vol. 48, no. IMAC-REVIEW-2009-001, pp. 133–140, 2010.↩︎
J. Geng, “Structured-light 3d surface imaging: a tutorial,” Advances in Optics and Photonics, vol. 3, no. 2, pp. 128–160, 2011.↩︎
S. S. Gorthi and P. Rastogi, “Fringe projection techniques: whither we are?,” Optics and Lasers in Engineering, vol. 48, no. IMAC-REVIEW-2009-001, pp. 133–140, 2010.↩︎
F.Deng,W.F.Sze,J.Deng,K.S.Fung,W.Leung,andE.Y.Lam,“Regularizedmultiframe phase-shifting algorithm for three-dimensional profilometry,” Applied optics, vol. 51, no. 1, pp. 33–42, 2012.↩︎
V. Srinivasan, H. Liu, and M. Halioua, “Automated phase-measuring profilometry of 3-d diffuse objects,” Applied optics, vol. 23, no. 18, pp. 3105–3108, 1984.↩︎
V. Srinivasan, H. Liu, and M. Halioua, “Automated phase-measuring profilometry of 3-d diffuse objects,” Applied optics, vol. 23, no. 18, pp. 3105–3108, 1984.↩︎
F.Deng,W.F.Sze,J.Deng,K.S.Fung,W.Leung,andE.Y.Lam,“Regularizedmultiframe phase-shifting algorithm for three-dimensional profilometry,” Applied optics, vol. 51, no. 1, pp. 33–42, 2012.↩︎
Yen, H.N., Tsai, D.M. and Yang, J.Y., 2006. Full-field 3-D measurement of solder pastes using LCD-based phase shifting techniques. IEEE Transactions on Electronics Packaging Manufacturing, 29(1), pp.50-57.↩︎
Xian, T. and Su, X., 2001. Area modulation grating for sinusoidal structure illumination on phase-measuring profilometry. Applied Optics, 40(8), pp.1201-1206.↩︎