向心加速度推导

角加速度

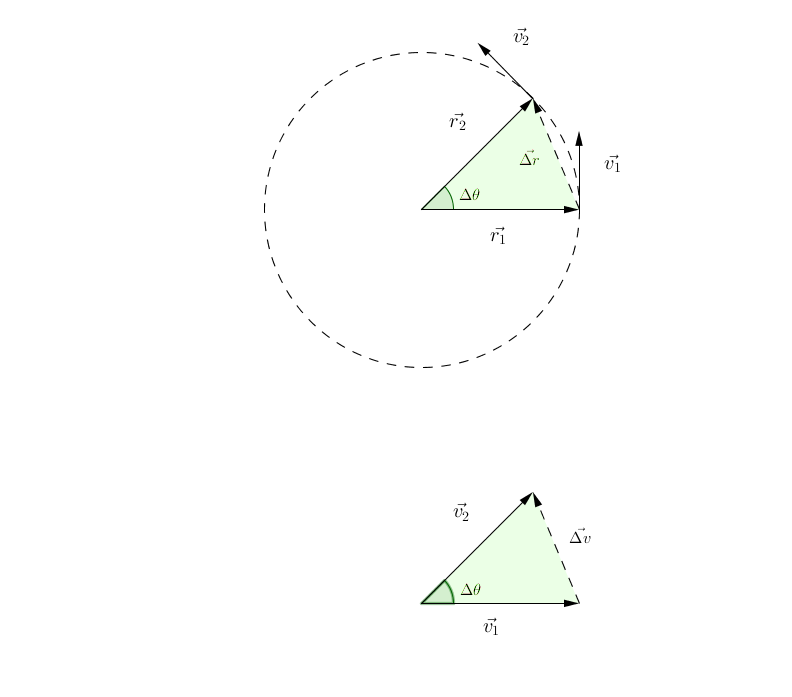
我们假设质点进行匀速圆周运动，有：\[\left| {\vec {v_1} } \right| = \left| {\vec {v_2} } \right|\]

因为两个绿色区域相似，有：\[\frac{\left| {\vec {\Delta r} } \right|}{\left| {\vec r} \right|} = \frac{\left| {\vec {\Delta v} } \right|}{\left| {\vec v} \right|}\] 因为路程＝速度*时间，当\(\theta \to 0\)时，有：\[\left| \vec {\Delta r} \right| = \left| {\vec v} \right|\Delta t\]

\[\frac{\left| \overrightarrow {\Delta r} \right|}{\left| \overrightarrow r \right|} = \frac{\left| {\vec v} \right|\Delta t}{\left| {\vec r} \right|} = \frac{\left| {\overrightarrow {\Delta v} } \right|}{\left| {\vec v} \right|}\]

\[\therefore \frac{ {\vec v}^2 \Delta t }{\left| \vec r\right|} = \frac{\left| \vec {\Delta v} \right|}{\Delta t} = \vec a \]

当\(t \to 0\)时成立。最后有：

\[\vec a = \frac{ {\vec v}^2}{\left| {\vec r} \right|}\overrightarrow n\]

\(\overrightarrow n\)为法向量，指向圆心；\(\vec a\)即为向心加速度。