一种基于KLT的直线段匹配算法

Posted on In , Views: Disqus:

罗汉杰. 直线段匹配方法、装置、存储介质及终端[P]. 中国专利: CN109919190A, 2019-06-21. Github: https://github.com/HanjieLuo/line_matching

背景

在计算机视觉系统中，其中一种重要任务是图像中的特征匹配。我们在多张图片中提取出一些特征纹理，并且将这些纹理匹配起来。在传统的方法中，我们一般使用梯度值大的，处于边角位置的点作为特征来进行匹配。但在实际使用中，图像中能够提取的，稳定的特征点是有限的。

我们发现，比起特征点，图像中的直线具有更强的稳定性和抗干扰能力；并且在室内等经典场景中，直线纹理出现的概率比特征点要多。

linematching1

而传统的基于描述子的直线匹配方法（如LBD1，MSLD2等），采用直线的局部外观特征和几何约束特征，对每一根直线段进行数学建模，然后进行匹配。但这些方法运算量巨大，难以满足实时任务的需求；并且，匹配的成功率也一般。

对于相继拍摄的前后两张图片，可以观察到特征纹理的偏移量较小。基于这个前提，我们可以对直线段使用一些本用于特征点的，高效的匹配方法来实现直线匹配功能。

本文提出了一种图像直线段的匹配方法，它使用了高效的一维光流法特征点匹配方法，对直线段上的点进行匹配操作，然后对匹配点进行统计，从而实现直线段跟踪的功能。

方法

直线检测

\(L_0= \lbrace ^0l_i \mid ^0l_i =(^0p_{i,0}, ^0p_{i,1}), 0≤i<M_0 \rbrace\)

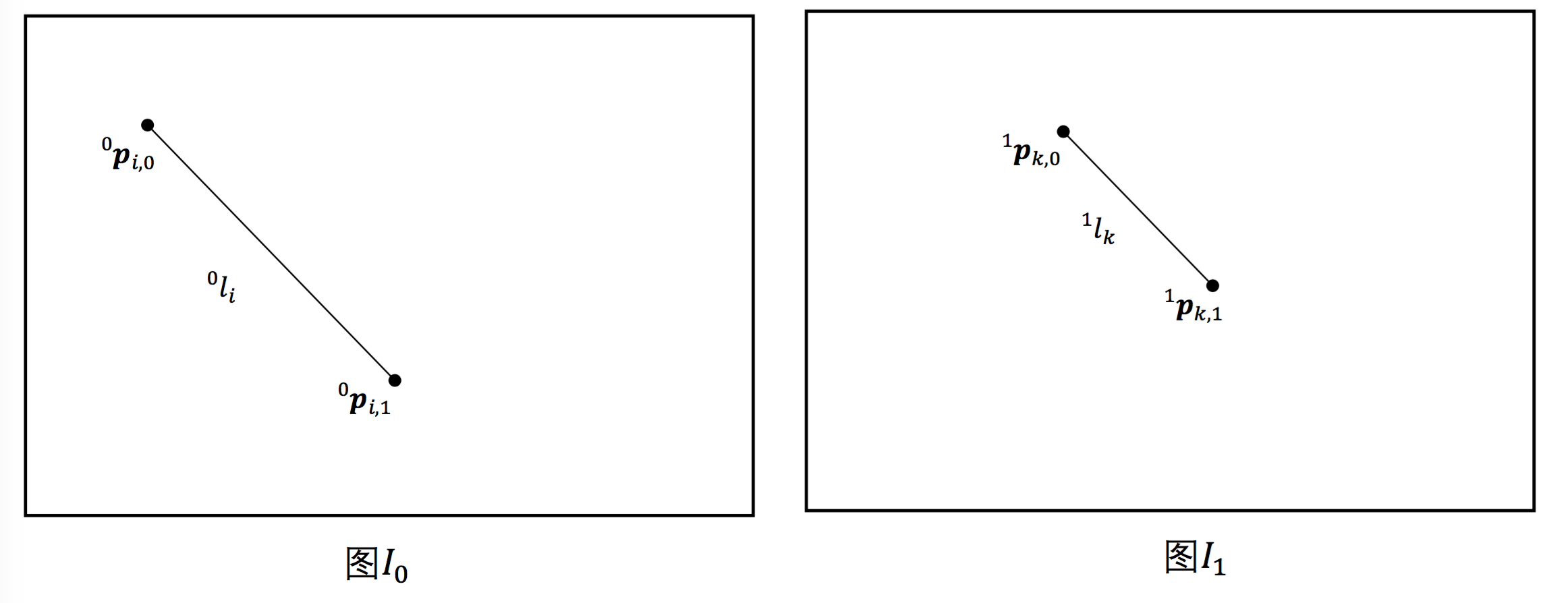
假设已知有前后相继拍摄的两张图片\(I_0\)和\(I_1\)。使用LSD3，EDLines45等直线检测算法，在图片\(I_0\)中获得直线段集合\(L_0= \lbrace ^0l_i \mid ^0l_i =(^0p_{i,0}, ^0p_{i,1}), 0≤i<M_0 \rbrace\)，\(M_0\)表示线段数目；\(^0p_{i,0}\)，\(^0p_{i,1}\)分别表示图\(I_0\)上第\(i\)根线段\(^0l_i\)的两个端点的二维坐标，\(p=[px,py]^T\)，\(T\)表示矩阵转置，\(p\)为一列向量。同样，我们图片\(I_1\)中获得直线段集合\(L_1= \lbrace ^1l_i \mid ^1l_i =(^1p_{k,0}, ^1p_{k,1}),0≤k<M_1 \rbrace\)。

linematching2

锚点匹配

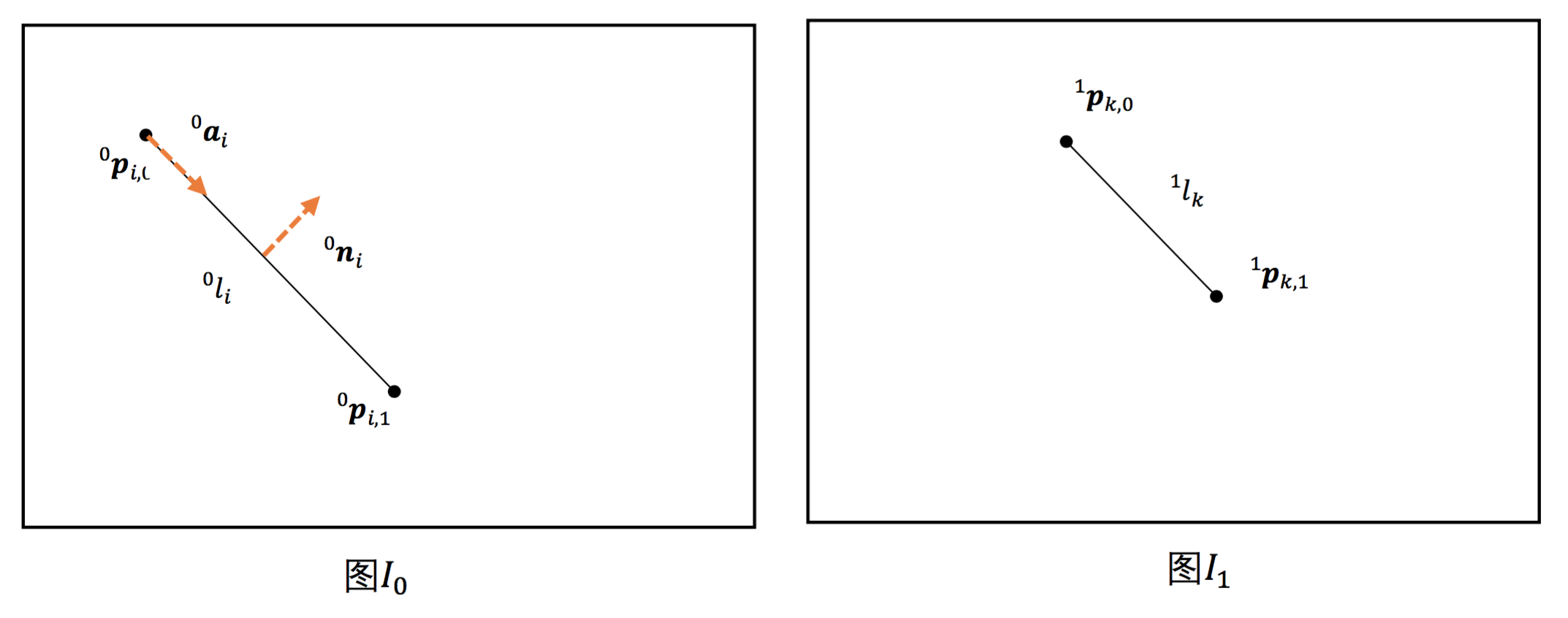
对图\(I_0\)上的每一条线段\(^0l_i ∈L_0\)，\(^0l_i =(^0p_{i,0}, ^0p_{i,1})\)：

  1. 计算线段的方向向量\(^0a_i =[^0a_{i,0}, ^0a_{i,1}]^T = (^0p_{i,1} -^0p_{i,0})/‖^0p_{i,1}-^0p_{i,0}‖\)和法向量\(^0n_i =[-^0a_{i,1}, ^0a_{i,0}]^T\)。
linematching3
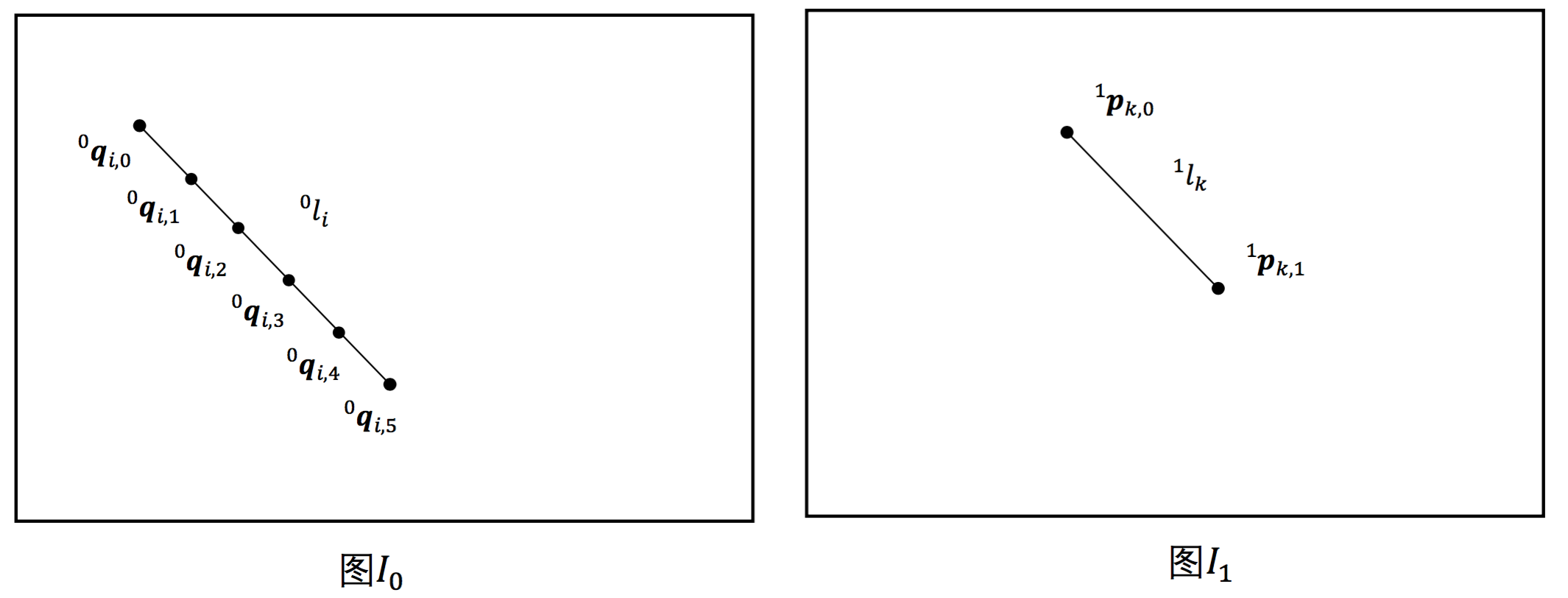
  1. 以\(^0p_{i,0}\)为起点，\(^0p_{i,1}\)为终点，\(^0a_i\)为方向，每隔距离\(s\)，选取一系列锚点，并将它们的坐标集合记作\(^0Q_{i} = \lbrace^0q_{i,j} \mid 0≤j<N_{i} \rbrace\)，\(N_i\)为线段\(^0l_{i}\)的锚点数目，\(s\)我们一般设置为20。
linematching4
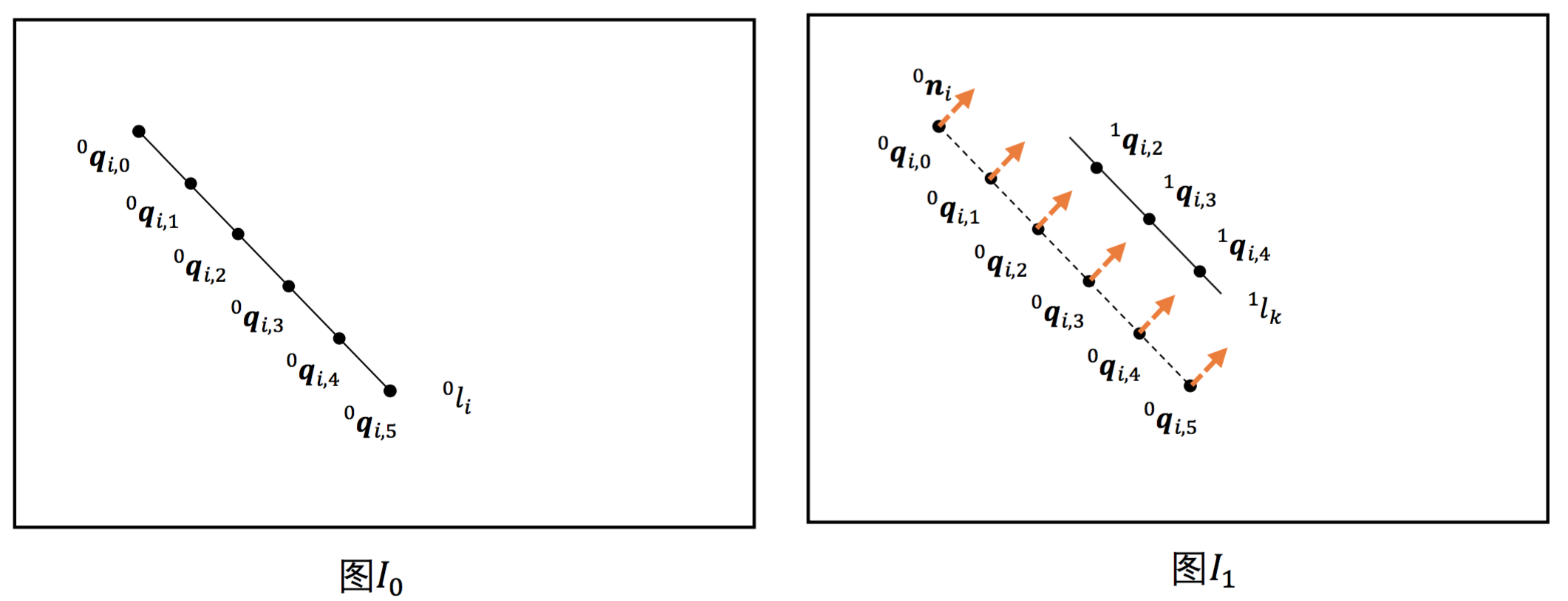
  1. 使用一维光流匹配法6，对图\(I_0\)线段\(^0l_{i}\)上每一个锚点\(^0q_{i,j}\)，在图\(I_1\)上，以\(^0q_{i,j}\)为起始位置，\(^0n_{i}\)为搜索方向，在图\(I_1\)上找到匹配点\(^1q_{i,j}\)。
linematching5

点-线匹配

经过上一个步骤后，我们在图\(I_1\)上找到图\(I_0\)上所有锚点\(^0q_{i,j}\)的匹配点\(^1q_{i,j}\)。在这一个步骤中，我们希望知道匹配点是属于图\(I_1\)上哪一条直线段的，我们称这一步骤为点-线匹配。

\(^0q_{i,j}\)为图\(I_0\)上的锚点，\(^1q_{i,j}\)为在图\(I_1\)上的相应匹配点；图\(I_1\)的直线段集合为\(L_1\)，\(L_1= \lbrace ^1l_{k} \mid ^1l_{k} =(^1p_{k,0}, ^1p_{k,1}), 0≤k<M_1 \rbrace\)。

对于任意点\(q\)，到直线段\(l=(p_0, p_1)\)有最短距离\(d\)：

\[\begin{aligned} v &= p_1 - p_0 \newline u &= p_0 - q \newline t &= min⁡(max⁡(-(v^T u)/(v^T v),0),1) \newline d &= ‖tv+u‖ \end{aligned}\]

其中\(v\)，\(u\)，\(t\)为中间变量。对于每一个匹配点\(^1q_{i,j}\)，做：

计算到图\(I_1\)所有直线段\(^1l_{k}\)的最短距离，获的距离集合$ d_k \(。比较\) d_k \(，获得的最短距离\)d_{min}=min⁡( d_k )\(和所对应的直线段\)^1l_{closest(i,j)}$，\(0≤closest(i,j)<M_1\)。如果\(d_{min}<d_{threshold}\)，则我们认为点\(^1q_{i,j}\)是属于直线\(^1l_{closest(i,j)}\)的。\(d_{threshold}\)为一经验阀值，我们设置为1。

通过上述步骤，我们获得了匹配点在图\(I_1\)上所对应的直线段。因此，每一个图\(I_0\)上的锚点，都有可能匹配到图\(I_1\)上的任一直线段。

线-线匹配

对于图\(I_0\)上的任意直线段\(^0l_i\)，\(0≤i<M_0\)，拥锚点\(^0q_{i,j}\)，\(0≤j<N_i\)；每一个锚点在图\(I_1\)上存在唯一的匹配点\(^1q_{i,j}\)，并且我们知道匹配点落在了图\(I_1\)的任一直线\(^1l_{closest(i,j)}\)上。

对于任一直线段\(^0l_i\)：

统计它拥有的锚点在图\(I_1\)所匹配直线段，假设最多有\(Z_i\)个锚点匹配到了直线\(^1l_{match(i)}\)上, \(0≤match(i)<M_1\)。如果\(Z_i/N_i >R\)，则我们称这两条直线\(^0l_i\)与直线\(^1l_{match(i)}\)互相匹配。\(R\)为一经验阀值，我们设置为0.4。

实验结果

Github: https://github.com/HanjieLuo/line_matching

  1. Zhang, Lilian, and Reinhard Koch. "An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency." Journal of Visual Communication and Image Representation 24.7 (2013): 794-805.↩︎

  2. Wang, Zhiheng, Fuchao Wu, and Zhanyi Hu. "MSLD: A robust descriptor for line matching." Pattern Recognition 42.5 (2009): 941-953.↩︎

  3. Von Gioi, Rafael Grompone, et al. "LSD: a line segment detector." Image Processing On Line 2 (2012): 35-55.↩︎

  4. Akinlar, Cuneyt, and Cihan Topal. "EDLines: A real-time line segment detector with a false detection control." Pattern Recognition Letters 32.13 (2011): 1633-1642.↩︎

  5. http://luohanjie.com/2021-02-03/edline-parallel.html↩︎

  6. http://luohanjie.com/2018-12-26/1d-klt-feature-tracker.html↩︎