用于SLAM的图像增强算法(算法原理)
罗汉杰. 图像增强方法、装置、计算机设备和存储介质 [P]. 中国专利: CN109801244A,2019-05-24.
Github: https://github.com/HanjieLuo/Image-Enhancement-for-SLAM
背景
图像处理,是指对图像进行分析和计算,使得图像满足工作的需要。在实际运用中,通过摄像头获得的图像往往会出现太暗,对比度太低的情况,使得无法进行后续的工作,特别是一些需要图像中纹理信息的工作。
现有的直方图均衡化是经常用于图像增强的算法。它根据累积分布函数对图像的灰度值进行操作,使得图像的灰度值均匀分布,从而提高图像的对比度。但直方图均衡化有一个很明显的缺点,由于它是一种全局优化,与具体纹理无关,使得增强后的图像会出现一些不自然的纹理。

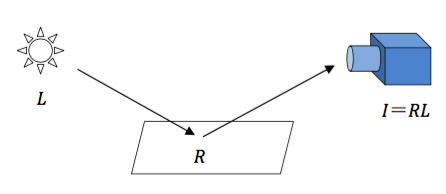
图像领域的Retinex理论中1,L代表环境光的照射分量,决定了图像像素能达到的动态范围,\(R\)表示携带图像细节信息的目标物体的反射分量,即图像内在属性。入射光\(L\)经过物体表面,根据反射率\(R\)进行反射,到达到观察者位置得到物体图像\(I\),即可表示为下式: \(I=RL\)。所以物体的成像灰度值不是由反射光强度\(L\)的值决定的,而是对光线的反射能力\(R\)决定的。
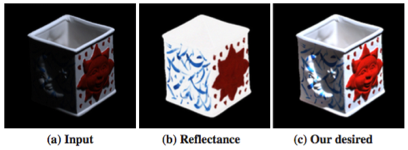
下图中2,(b)表示了\(R\)图,它去除了由于光线照射影响而产生的纹理,是物体最原始的样貌;(a)表示了\(R\)图基础上加上环境光\(L\)后产生的图像\(I\);(c)我们的目标不是百分百恢复出\(R\)图,而是通过近似恢复\(R\)图,来获得增强图(c)。它比起原图\(I\),去掉了很多由于环境光\(L\)分量而造成的阴影区域,恢复出了更多物体原有信息。
基于Retinex理论的图像增强目的就是从原始图像\(I\)中估计出光照\(L\),根据\(R=I/L\)分解出\(R\),而\(R\)就是我们所需的图像增强图。

本文提出了一种基于Retinex理论的图像增强算法,对欠曝光的图像进行增强, 能够恢复图像中的纹理,并且做到实时处理。
方法
光照图\(L\)估算
我们无法直接从图像\(I\)中获得光照图\(L\)。一个好的仿光照图中,它能够保持图\(I\)中物体的结构,并且消除图像中的细节纹理3。
参照Dongbo Min提出的FGS图像图像平滑法4,我们将光照图\(L\)求取问题改为一个优化方法,给定一张灰度图\(I\)和对应的归一化图\(N=‖I‖\),通过最小化下面的加权最小二乘公式\(J(L)\),获得光照图\(L\):
\[\begin{align} J(L)=\sum_{p}\left(\left(L_{p}-N_{p}\right)^{2}+\lambda \sum_{q \in \mathcal{N}(p)} w_{p, q}(I)\left(L_{p}-L_{q}\right)^{2}\right) \end{align}\]
其中,\(p=(x,y)\),\(0≤x<W\),\(0≤y<H\)为像素位置,\(W\)为图\(I\)的宽,\(H\)为高。\(N(p)\)表示位置\(p\)的邻近位置(一般取\(4*4\)区域)。\(λ\)为控制参数,\(λ\)值越大,输出光照图\(L\)越平滑,我们一般设置为15。\(w_(p,q)(I)\) 为权重函数,为一高斯函数,定义为:
\[\begin{align} w_{p, q}(I)=\exp \left(-\left(I_{p}-I_{q}\right)^{2} / \sigma\right) \end{align}\]
\(exp\)为指数函数;\(σ\)为控制参数,我们一般设置为10。权重函数的作用是,对于梯度值高的像素(物体边缘),我们给予一个较小的权值;对于梯度值低的像素,我们给予一个较大的权值。通过这样设置,最小化\(J\)后获的光度图\(L\)中,物体边缘获得保持,其余纹理得到平滑。
代价函数\(J(L)\)包括两个部分,\(\left(L_{p}-N_{p}\right)^{2}\)项会使得得到的\(L\)趋向于与归一化后的\(I\)图一致;\(\lambda \sum_{q \in \mathcal{N}(p)} w_{p, q}(I)\left(L_{p}-L_{q}\right)^{2}\)项会消除\(L\)图像中的细节纹理,但会保持物体的边缘纹理。
为了最小化\(J(L)\),将\(J(L)\)的导数为0 ,然后可以通过解下面的线性方程组获得光度图\(L\):
\[\begin{align} L=(\Theta+\lambda A)^{-1} N \end{align}\]
这里,\(Θ\)为单位矩阵,而\(A\)为一个\(S×S,S=W×H\)的二维矩阵:
\[\begin{align} A(m, n) = \begin{cases} \sum_{l \in \mathcal{N}(n)} w_{m, l}(I), & \text{n=m} \newline -w_{m, n}(I), & n \in \mathcal{N}(m) \newline 0, & \text{其余} \end{cases} \end{align}\]
注意这里\(L\)和\(N\)为了计算方便,由\(W×H\)的二维矩阵变成一个\(S×1\)的一维向量(列头尾相接)。
在获得光照图\(L\)后,我们可以根据\(R=I/L\)获得增强图\(R\)。为了调整图\(R\)的亮度,我们对光照图\(L\)进行一次\(Gamma\)校正,使得\(R=I/L^γ\)。这里,我们一般将\(γ\)设置为0.5到0.7之间。

去噪
对原图\(I\)增强,原图的噪音也相应地增强了,所以增强图R中有比较明显的噪音,需要对增强图\(R\)进行一次去噪处理。考虑到去噪效果和性能,我们使用了双边滤波对增强图\(R\)进行去噪,双边滤波的优点是能够保持图像的边缘信息。也可以尝试其他的去噪算法,如高斯滤波,中值滤波等,但效果没有双边滤波好。

对比度增强
增强图\(R\)能够很好地恢复出原图中欠曝光区域的纹理信息,但图像的整体对比度较低。为了提高图片的对比度,我们在这里进行一次对比度增强处理。增强图\(R\)的概率密度函数为:
\[\begin{align} p d f(l)=n_{l} /(W * H) \end{align}\]
其中,\(n_l\)为增强图\(R\)中灰度值为\(l\)的像素的数目。图像的累积分布函数为:
\[\begin{align} c d f(l)=\sum_{k=0}^{l} p d f(k) \end{align}\]
然后我们定义两个阀值\(t_{low}\)和\(t_{high}\),为0到1之间的一个概率值, \(t_low<t_high\)。我们再定义\(l_{low}\)为\(cdf(l_{low})≈t_{low}\),即累积分布函数约等于给定的\(t_{low}\)值时应对的灰度值l设置为\(l_{low}\)。同样,我们得到\(l_{high}\),\(cdf(l_{high})≈t_{high}\)。一般我们将\(t_{low}=0.01\),\(t_{high}=0.99\)。
然后我们对增强图\(R\)上的像素点根据下式进行映射:
\[\begin{align} R(p) = \begin{cases} 0, & R(p)<l_{low} \newline 255, & R(p)>l_{high} \newline 255(R(p)-l_{low})/(l_{high}-l_{low}), & \text{其余} \end{cases} \end{align}\]
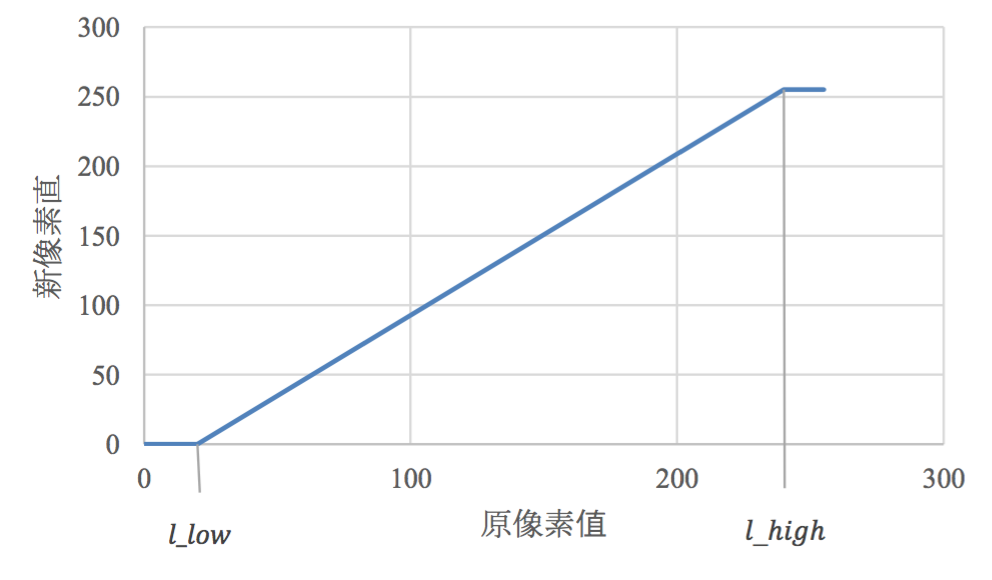
通过上图可见,我们对于增强图\(R\)中灰度值低于\(t_{low}\)的像素置零,高于\(t_{high}\)的置为255,其余的点进行一次线性变化。通过这样,达到了增强对比度的效果。

实验结果

更多的实验结果可以参照上一篇博客《用于SLAM的图像增强算法》。
Github: https://github.com/HanjieLuo/Image-Enhancement-for-SLAM
Land, Edwin H. "The retinex theory of color vision." Scientific american 237.6 (1977): 108-129.↩︎
Guo, Xiaojie, Yu Li, and Haibin Ling. "LIME: Low-light image enhancement via illumination map estimation." IEEE Transactions on Image Processing 26.2 (2017): 982-993.↩︎
Guo, Xiaojie, Yu Li, and Haibin Ling. "LIME: Low-light image enhancement via illumination map estimation." IEEE Transactions on Image Processing 26.2 (2017): 982-993.↩︎
Min, Dongbo, et al. "Fast global image smoothing based on weighted least squares." IEEE Transactions on Image Processing 23.12 (2014): 5638-5653.↩︎