机械臂实时停止S型(Double S)速度规划算法
罗汉杰. 一种机械臂的运动轨迹规划方法、装置及机器人:中国,201610453116[P/OL]. 2016-06-20 [2018-08-22]. https://patentimages.storage.googleapis.com/1c/c7/07/cb789c3bd3adfc/CN105922265A.pdf
Introduction
机械臂的轨迹规划程序中,程序会接受用户提供的起点,终点位置信息,然后程序会在两点之间生成一系列的插补点来描述机械臂应该运行的轨迹。
示教功能是一种可重复再现通过示教编程存储起来的作业程序的功能,是机械臂的基础功能之一。示教编程有很多种实现方式,其中一种是人工利用示教盒对机械臂发送指令,使得机械臂完成预期动作来完成动作编程。
在这些指令中,最常用的就是令机械臂一直沿某个给定的方向走直线运动,直到用户发送停止指令或者超出工作范围为止。但在示教功能中,终点位置是由用户实时决定的,所以轨迹规划程序不能将整个运动过程提前规划。由于机械臂的速度和加速度总是从零开始,然后在终点又恢复为零,所以在示教功能中,轨迹规划程序单接收到停止指令后,需要马上规划出一段平滑的减速轨迹。
在普通的轨迹规划中,大多使用简单的三次多项式插值的方法,该方法的缺点是插值出来的轨迹在加速度上不连续,使得机械臂运行时会产生震动,从而影响精度和使用寿命。 而传统的基于S型(Double S)速度规划算法所得的轨迹在加速度上连续, 所以运行时十分平稳,已经广泛使用在机床,机械臂等的轨迹规划功能上。
本文提出了一种用于示教的减速阶段的基于S型速度规划算法,令机械臂能够平稳并且迅速地停止下来。
S型(Double S)速度规划算法
下图显示了一种经典的S型速度规划的行程\(q\),速度\(v\),加速度\(a\),加速度的导数(\(jerk\))\(j\)曲线图。在S型速度规划算法中,一般会有以下假设:
\[\begin{aligned} j_{min}=-j_{max}, a_{min}=- a_{max}, v_{min}=- v_{max} \end{aligned}\]
min和max分别表示为最小值和最大值。
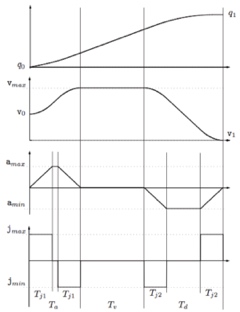
S型速度规划中整个行程的时间\(t\)可分为3个阶段: 1. 加速阶段:\(t∈[0,T_a ]\),在这阶段中,加速度会从0开始,以恒定的\(j_{max}\)比例线性增加到最大值然后有下降回0。 2. 匀速阶段:\(t∈[T_a,T_a+T_v]\),此阶段保持匀速。 3. 减速阶段:\(t∈[T_a+T_v,T]\),其中\(T=T_a+T_v+T_d\),此阶段是跟加速度阶段相反的减速阶段,最终加速度回到0。
其中我们定义: \(T_{j1}\):在加速阶段中,\(jerk\)保持恒定(\(j_{max}/j_{min}\))的时间段 \(T_{j2}\):在减速阶段中,\(jerk\)保持恒定(\(j_{max}/j_{min}\))的时间段 \(T_a\):加速阶段 \(T_v\):匀速阶段 \(T_d\):减速阶段 \(T\):总用时 \(a_{lim_a}\):加速阶段最大加速度 \(a_{lim_d}\):减速阶段最小加速度 \(v_{lim}\):最大速度 \(q_0\):初始行程 \(q_1\):终点行程 \(v_0\):初始速度 \(v_1\):终点速度 \(a_0\):初始加速度 \(a_1\):终点加速度
由此可知,S型速度规划的特定是能够使得机械臂平滑加速到最大运行速度,然后又平滑地减速,而且总体用时最少。在我们实际使用中,一般会令到起点和终点的速度,加速度都为0,即\(v_0=v_1=0\),\(a_0=a_1=0\),下文我们都会采用这作为默认条件以简化公式。
在进行轨迹规划前,需要计算出曲线的参数。下图为S型速度规划的参数计算流程图:
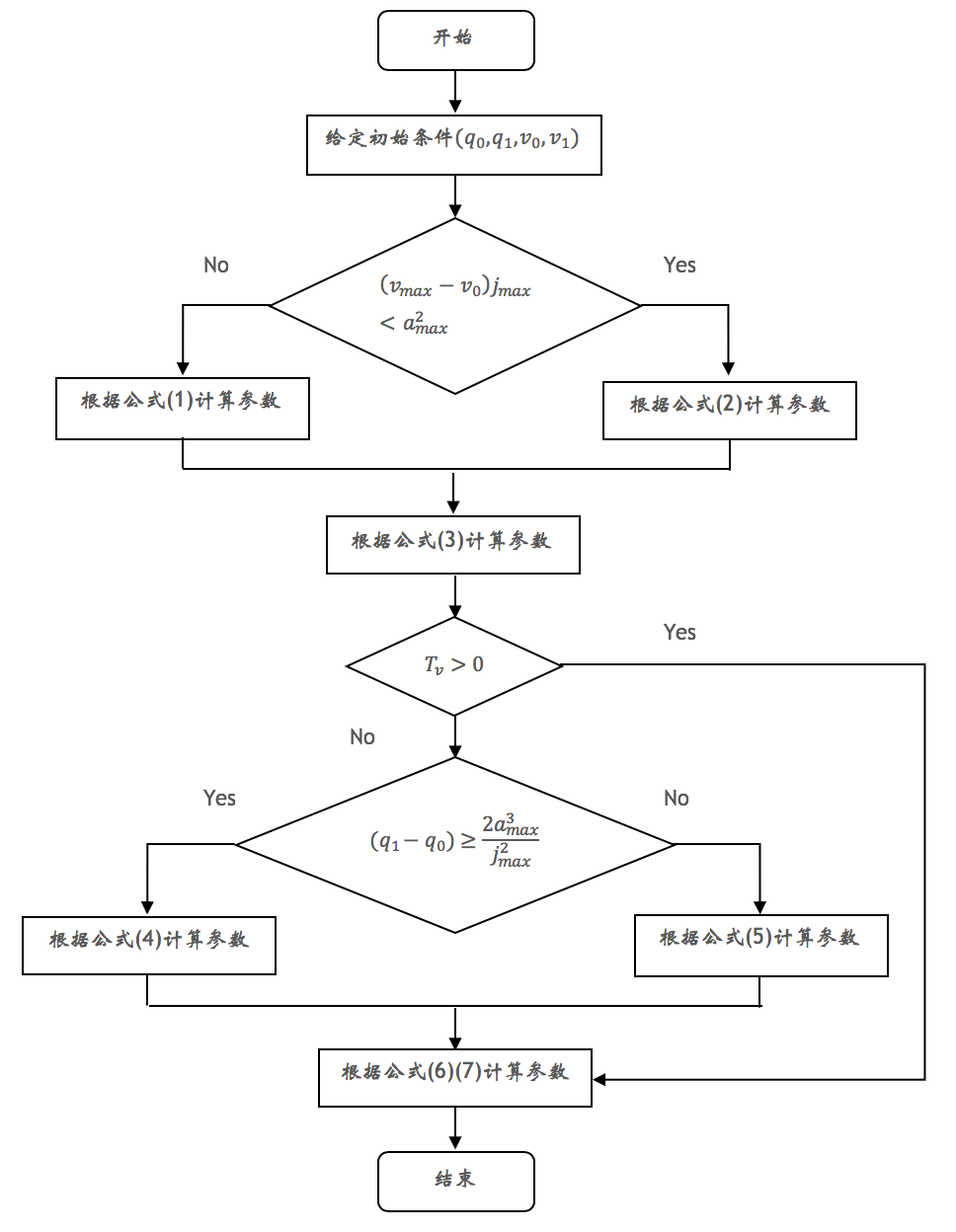
其中:
\[\begin{align} T_{j1}=T_{j2}=\frac{a_{max}}{j_{max}}, \quad T_a=T_d=T_{j1}+\frac{v_{max}}{a_{max}} \end{align}\]
\[\begin{align} T_{j1}= T_{j2}=\sqrt{\frac{v_{max}}{j_{max}}}, \quad T_a= T_d=2T_{j1} \end{align}\]
\[\begin{align} T_v=\frac{q_1-q_0}{v_{max}} - T_a \end{align}\]
\[\begin{align} T_v=0, \quad T_{j1}=T_{j2}=T_j=\frac{a_{max}}{j_{max}} \newline T_a=T_d=\frac{T_j}{2} + \sqrt{\frac{T_j^2}{4} + \frac{q_1-q_0}{a_{max}}} \notag \end{align}\]
\[\begin{align} T_v=0, \quad T_{j1}=T_{j2}=T_j=\sqrt[3]{\frac{q_1-q_0}{2j_{max}}}, \quad T_a=T_d=2T_j \end{align}\]
\[\begin{align} T=T_a+T_d+T_v, \quad a_{lim_a}&=j_{max}T_{j1}, \quad a_{lim_d}=-a_{lim_a} \newline v_{lim}&=(T_a-T_j1)a_{lim_a} \notag \end{align}\]
\[\begin{align} t_0=0, \quad t_1&=T_{j1}, \quad t_2=T_a-T_{j1}, \quad t_3=T_a \newline t_4=T_a+T_v, \quad t_5&=t_4+T_{j2}, \quad t_6=T_v-T_{j2}, \quad t_7=T_v \notag \end{align}\]
所以,S型速度规划算法整个流程如下:
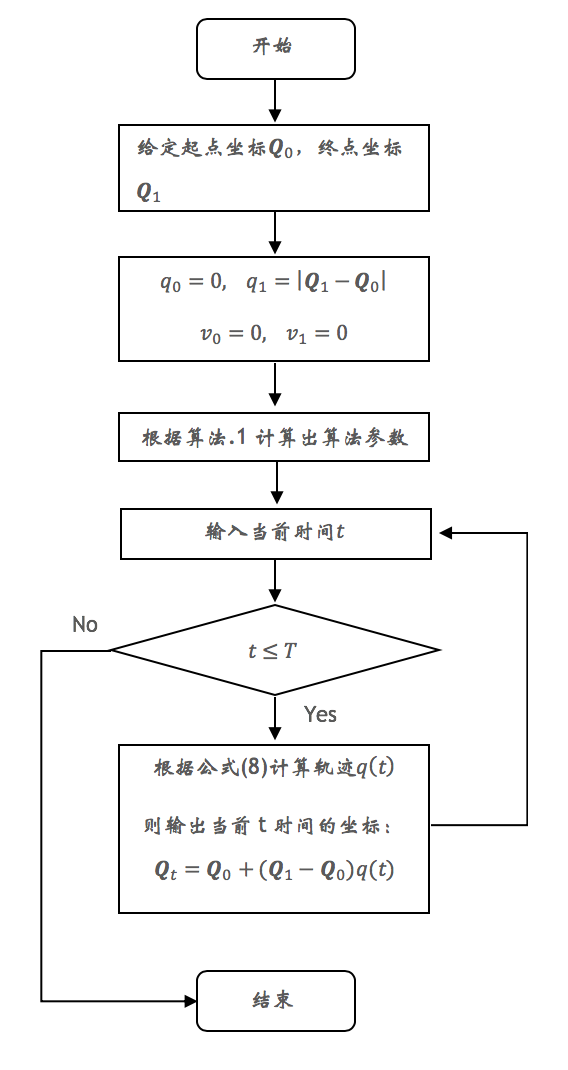
其中: \[\begin{align} q(t) &= \begin{cases} q_0+(j_{max} t^3)/6, & t∈[t_0,t_1) \newline q_0+ a_{lim_a}(3t^3-3T_{j1}t+T_{j1}^2)/6, & t∈[t_1,t_2) \newline q_0+v_{lim}T_a/2-v_{lim}(T_a-t)-j_{min}(T_a-t)^3/6 & t∈[t_2,t_3) \newline q_0+v_{lim}T_a/2+v_{lim} (t-T_a ), & t∈[t_3,t_4) \newline q_1-v_{lim}T_d/2+v_{lim}(t-T+T_d)-j_{max}(t-T+T_d)^3/6, & t∈[t_4,t_5) \newline q_1-v_{lim}T_d/2+v_{lim}(t-T+T_d)+a_{lim_d}(3(t-T+T_d)^2 & t∈[t_5,t_6) \newline \quad -3T_{j2}(t-T+T_d)+T_{j2}^2)/6 \newline q_1-j_{max}(T-t)^3/6, & t∈[t_6,t_7) \end{cases} \end{align}\]
实时停止 S 型(Double S)速度规划算法
假设我们使用上述算法进行机械臂轨迹规划,当运行到\(𝑡\)时刻,\(0 ≤ 𝑡 ≤ 𝑇\)时,我们想让机械臂停止下来。此时需要算法在当前的运行状态下马上规划出一段合适的减速阶段,令机械臂能够平稳并且迅速地停止下来。 算法如下:
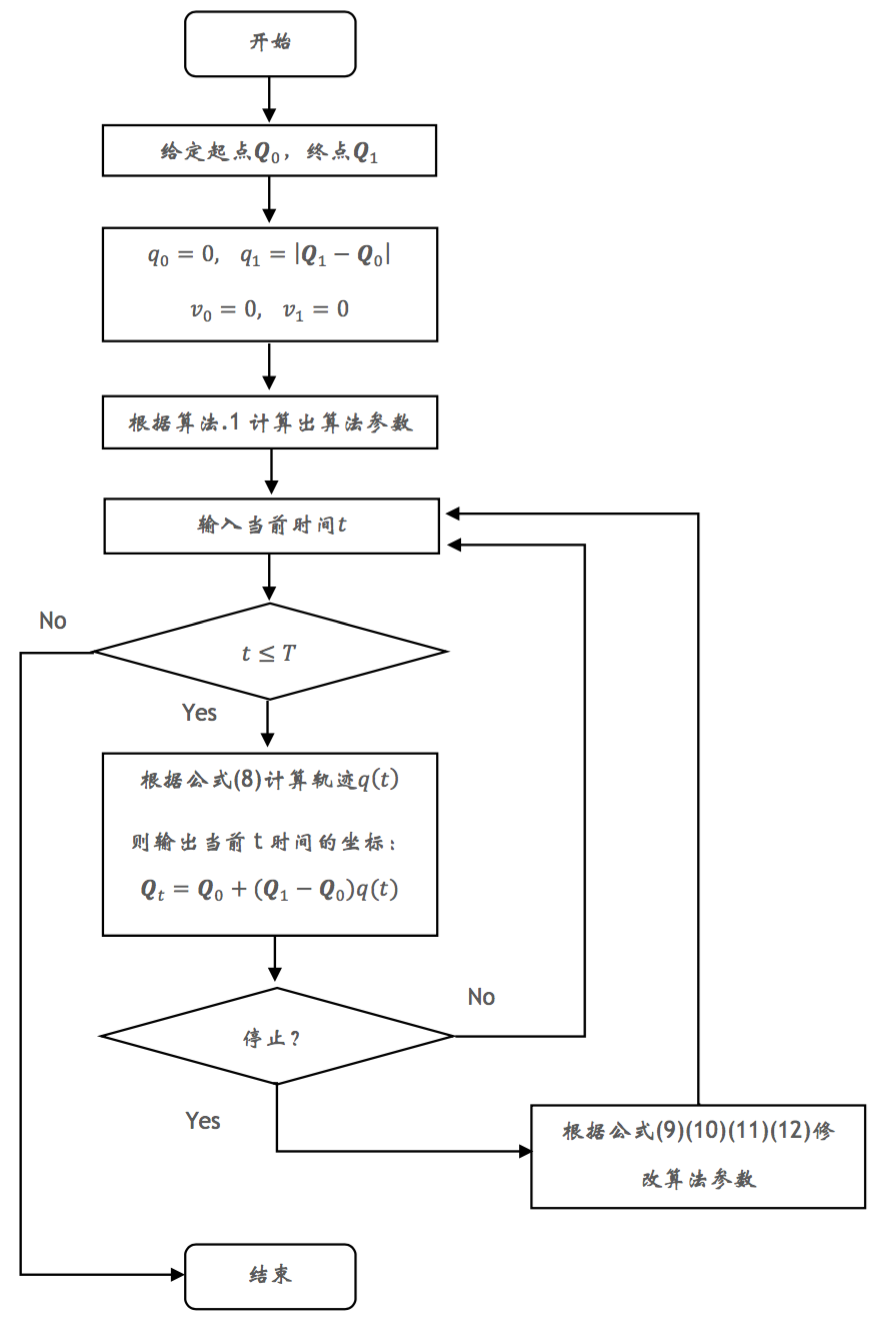
1. 如果\(t∈[t_0,t_1)\)
\[\begin{align} T_{j1}=T_{j2}= T_j =& t, \quad T_a=T_d=2T_j, \quad T_v=0 \notag\newline a_{lim_a} = j_{max}&T_{j1}, \quad a_{lim_d}=-a_{lim_a} \notag \newline v_{lim} &= T_{j1}a_{lim_a} \newline q_1 &= T_{j1}a_{lim_a}T_a \notag \newline t_1=T_{j1}, \quad t_2 &= t_1, \quad t_3=t_2+T_{j1}, \quad t_4=t_3 \notag \newline t_5=t_3+T_{j2}, \quad t_6 &= t_5, \quad t_7=t_6+T_{j2}, \quad T=t_7 \notag \end{align}\]
2. 如果\(t∈[t_1,t_2)\)
\[\begin{align} T_a=T_a-(t_2-t), \quad &T_d=T_a, \quad T_v=0 \notag \newline v_{lim}=(T_a-T_{j1}& ) j_{max} T_{j1} \notag \newline q_1=(T_a-T_{j1}&)a_{lim_a}T_a \newline t_2=t, \quad t_3&=T_a, \quad t_4=t_3 \notag \newline t_5=t_4+T_{j2}, \quad t_6=T_a+t&, \quad t_7=t_6+T_{j2}, \quad T=t_7 \notag \end{align}\]
3. 如果\(t∈[t_2,t_3)\)
\[\begin{align} q_1= q_1 &-v_{lim} T_v \notag \newline t_4=t_3, \quad t_5= t_5&-T_v, \quad t_6=t_6-T_v \newline t_7=t_7-T_v, \quad &T=t_7, \quad T_v=0 \notag \end{align}\]
4. 如果\(t∈[t_3,t_4)\)
\[\begin{align} q_1 = q_0 &+ v_{lim} t \notag \newline T_v=t-t_3, \quad t_4 &= t, \quad t_5=t_5-(t_4-t) \newline t_6=t_6-(t_4-t), \quad t_7&=t_7-(t_4-t), \quad T=t_7 \notag \end{align}\]
在示教功能中,用户会输入起始点和移动方向,并期盼机械臂一直沿该方向一直移动,直到用户下达停止指令或者已经到达边工作区域缘为止。
程序一开始,可以根据起始点\(Q_0\)和移动方向计算出该方向上的工作区域边缘位置,并将该点做为作为终点\(Q_1\)。
将\(Q_0\),\(Q_1\)输入到算法3中,程序会规划出一条移动轨迹,并且输出每一个时间点t时机械臂应该所在的位置\(Q_t\)。
机械臂会根据\(Q_t\)进行移动。
这时有两种情况:1. 用户在机械臂移动过程中某个时刻\(t\)发送了停止指令,算法3会马上对轨迹进行修改,令到机械臂马上开始减速,并且最终停止下来。2. 用户一直没有按停止指令,则机械臂在到达边缘位置时就会自动停止下来。