一种带过渡段的机械臂的轨迹规划算法
罗汉杰. 机械臂的控制方法和装置:中国,201610984458[P/OL]. 2017-03-01 [2018-03-20]. https://patentimages.storage.googleapis.com/7c/c5/c2/165019b55f0bee/CN106346478A.pdf
Introduction
机械臂的轨迹规划程序中,程序会接受用户提供的起点,终点位置信息,然后程序会在两点之间生成一系列的插补点来描述机械臂末端应该运行的轨迹。
当用户提供多条直线线段,并且要求机械臂末端依次沿着直线运行时,程序需要在每两条线段的手尾位置规划出一个过渡段,使得机械臂终端能够平稳地从一个运动方向转到另一个运动方向。为保证机械臂运行效率和精度,需要机械臂在整个运行过程中位移,速度,加速度参数必须连续。
本文提出了一种用于机械臂的轨迹规划算法,能够使得机械臂从当前状态开始规划出一条位移,速度,加速度连续的过渡轨迹,到要运行的直线轨迹上。
Approach
给定机械臂目标直线的起点\(P_1\),终点 \(P_2\)。其中\(P\)表示笛卡尔坐标系下的位置参数\(P_i=[x_i,y_i,z_i ]^T\)。给定当前的机械臂关节空间角度\(Q_0=[q_0,q_1,…,q_n ]^T\),其中\(n\)为机械臂的关节数目,同理给定机械臂关节角速度\({\dot Q_0}\),关节角加速度\({\ddot Q_0}\)。
使用S 型(Double S)速度规划/多阶样条插值/b样条插补等方法,规划出直线线段\(P_1 P_2\)在笛卡尔坐标系下的插补点\(P_t=[x_t,y_t,z_t ]^T\),速度\(\dot P_t=[\dot x_t,\dot y_t,\dot z_t ]^T\),加速度\(\ddot P_t=[\ddot x_t,\ddot y_t,\ddot z_t ]^T\),\(t\)为时间点,总运行时间为\(t_{line\_all}\)。
给定参数时刻\(t_s (0≤t_s≤t_{line\_all})\)(可根据给定的一个比例参数\(r_s\) 获得参数\(t_s=t_{line\_all}*r_s)\),并从已规划出的直线\(P_1 P_2\)上,获得时刻\(t_s\)时的坐标点\(P_s\),速度\(\dot P_s\),加速度\(\ddot P_s\),将此点作为过渡段的终点。
使用逆运动学方法,将笛卡尔坐标系下的\(P_s\)转换到此时刻关节空间下的参数\(Q_s\)。使用以下公式将\(\dot P_s\), \(\ddot P_s\)转换为\(\dot Q_s\),\(\ddot Q_s\):
\[\begin{align} \label{e1} \dot Q &= J^+ \dot P \newline \label{e2} \ddot Q &= J^+ (\ddot P- \dot J \dot Q) \end{align}\]
其中,\(J\)为雅可比(Jacobian)矩阵,\(\dot J\)为雅可比矩阵的一阶导,\(J^+\)为\(J\)的伪逆(Pseudoinverse)。
使用基于多阶多项式/三角函数等的曲轨迹生成方法,在以\(Q_0\),\(\dot Q_0\), \(\ddot Q_0\)为起点,\(Q_s\),\(\dot Q_s\), \(\ddot Q_s\)为终点,在轴空间规划出一条连续过度段轨迹,整个运行时长为\(t_{trans}\)。以五阶多项式曲线为例,先代入以下公式计算出系数参数:
\[\begin{align} a_0 &= Q_0 \notag \newline a_1 &= \dot Q_0 \notag \newline a_2 &= \ddot Q_0 / 2 \notag \newline a_3 &= \frac{20h-(8\dot Q_s+12\dot Q_0 ) t_{trans}-(3\ddot Q_0- \ddot Q_s ) t_{trans}^2 }{2t_{trans}^3} \newline a_4 &= \frac{-30h+(14\dot Q_s+16\dot Q_0 ) t_{trans}+(3\ddot Q_0-2\ddot Q_s ) t_{trans}^2}{2t_{trans}^4 } \notag \newline a_5 &= \frac{12h-6(\dot Q_s+\dot Q_0 ) t_{trans}+(\ddot Q_0-\ddot Q_s ) t_{trans}^2}{2t_{trans}^5 } \notag \label{e3} \end{align}\]
然后就可以根据以下公式计算出任意时刻\(t(0≤t≤t_{trans})\)时的关节角位置\(Q_t\),角速度\(\dot Q_t\),角加速度\(\ddot Q_t\):
\[\begin{align} \label{e4} Q_t&=Q_0+a_1 t+a_2 t^2+a_3 t^3+a_4 t^4+a_5 t^5 \newline \label{e5} \dot Q_t&=a_1+2a_2 t+3a_3 t^2+4_4 t^3+5a_5 t^4 \newline \label{e6} \ddot Q_t&=2a_2+6a_3 t+12a_4 t^2+20a_5 t^3 \end{align}\]
该过渡段的重点是,当运行到过渡段的终点时,此时的\(Q_{trans}\),\(\dot Q_{trans}\),\(\ddot Q_{trans}\),与在步骤2规划的直线线段在时刻\(t_s\)时的\(Q_s\),\(\dot Q_s\),\(\ddot Q_s\)相等,从而保证了位置,速度和加速度在数值上的连续。
所以,整个路径规划出来的线段包括过渡段和直线轨迹两个部分,其中过渡段用时\(t_{trans}\),直线段用时\(t_{line}\),总用时\(t_{all}\),其中:
\[\begin{align} \label{e7} t_{line} & =t_{line\_all}-t_s \newline \label{e8} t_{all} & =t_{trans}-t_{line} \end{align}\]
Flow Diagram
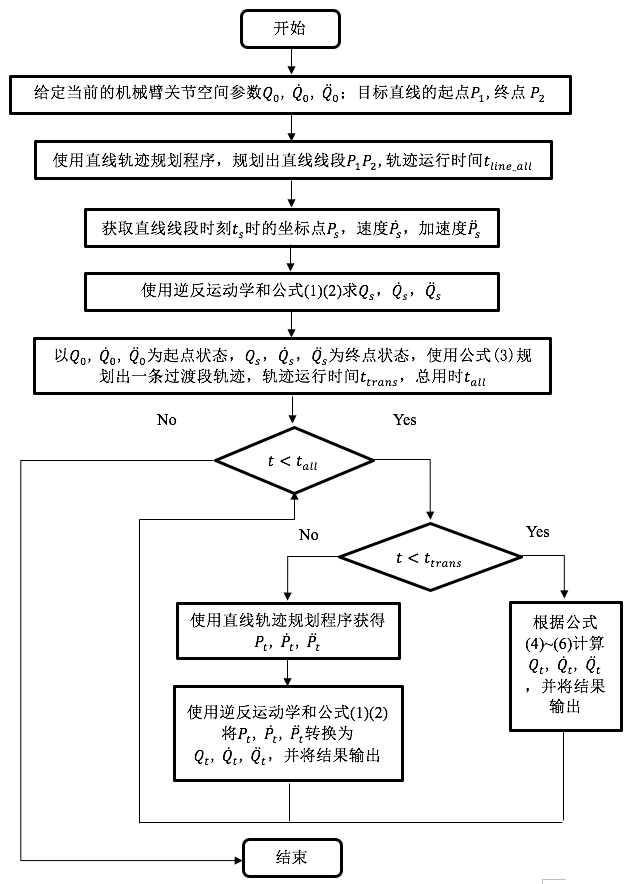
Experiment
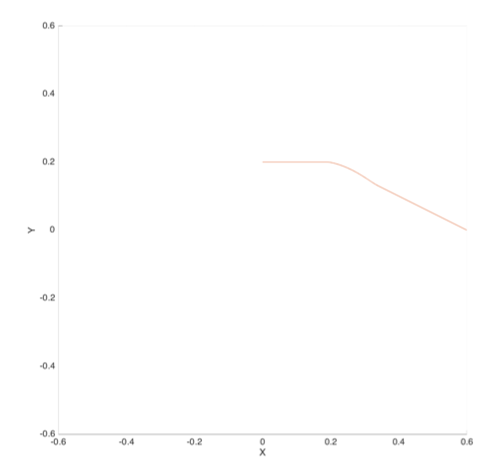
下图显示了SCARA型四轴机械臂末端从坐标\([0.6,0,0]^T\)直线运行到\([0.344,0.128,0]^T\),然后使用上文提出的算法,从当前位置规划出一个过渡段曲线到\([0.189,0.2,0]^T\),然后直线运行到终点\([0,0.2,0]^T\)。
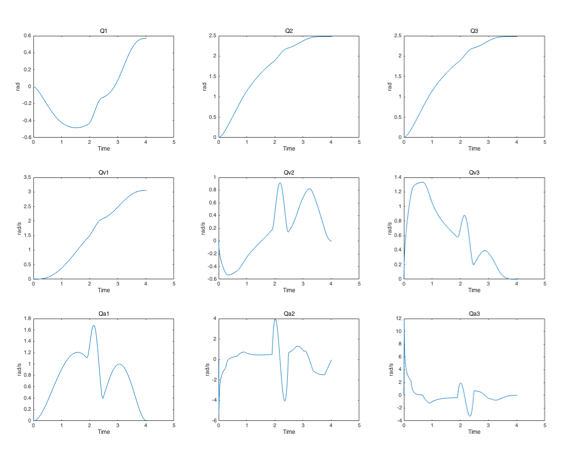
下图显示了机械臂的前三个轴各自在各个时刻的\(Q_t\),\(\dot Q_t\),\(\ddot Q_t\)。从图可以看到,无论是轴的角度,角速度,角加速度都连续。
Conclusion
在传统的机械臂中,当要连续执行多条直线轨迹的时候,需要先执行完一条轨迹,然后停止,再执行另外一条,这种运动方式效率十分低。
另外一些机械臂中,需要预先给出所有要运行的线段,然后才能在必要的地方规划出过渡段。
在本方法中,过渡段只与机械臂当前状态,起点,终点有关,不需要其余信息,方便使用;在整个运行过程中,机械臂不需要停止,规划出来的轨迹平稳,效率高。