SCARA型机械臂工作区域边界计算方法

Posted on 2016-11-15 In Tech , Robotics Views: Disqus:

罗汉杰. 一种机械臂的轨迹规划方法及装置：中国，201610452034[P/OL]. 2016-11-23 [2018-03-20]. https://patentimages.storage.googleapis.com/8a/5f/bc/325d10a3dee6fc/CN106041941A.pdf

SCARA(Selective Compliant Articulated Robot for Assembly)型机械臂是机械臂的一种。它拥有4个关节(图.1)，其中$J_1$，$J_2$，$J_4$为转动关节，$J_3$为滑动关节。

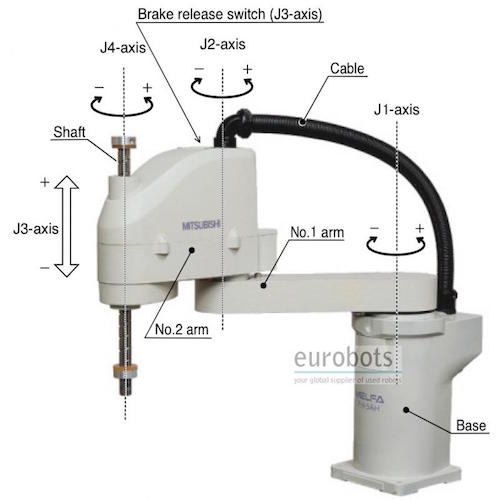
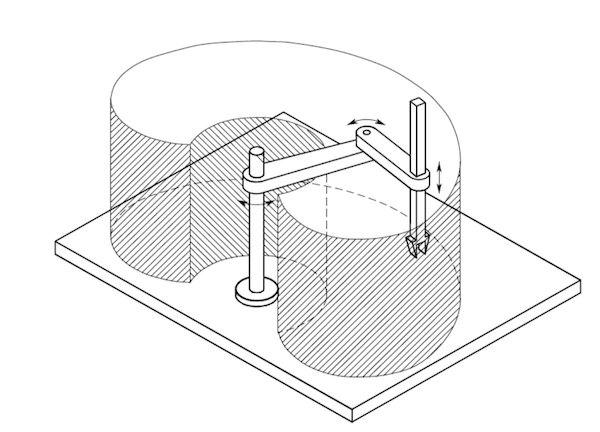
图. 1: SCARA型机械臂。

图. 2: SCARA型机械臂工作区域。

图.2显示了机械臂的工作空间。在机械臂工作的过程中，很多任务需要知道机械臂可到达的边缘位置，比如在示教功能中，用户通过手持设备发送指令，使得机械臂一直沿某个方向直线运动，直至到达到工作区域的边缘时，速度和加速度将降为零。

传统的方法中，可以通过不断监测当前机械臂的是否已经是到达极限位置来实现。但是这种方法需要对路径上所有的位置点进行检测，效率低，计算量大。

在本文中，我们提出了一种基于几何的方法来确定SCARA型机械臂工作区域边缘的方法。给定起始点和方向后，能给出与该射线相交的最近的工作区域边缘位置。利用该方法，在机器人运动前就可以提前知道终点的位置，方便机器人进行运动学规划。

数学模型

我们按照图.3所示对SCARA型机械臂进行DH(Denavit-Hartenberg)坐标系分配。其中转动关节$J_i$的转动轴与各自的$z_i$轴互相平衡，臂长为$\alpha _i$，$\lbrace i\mid i \in \lbrace 1,2,4 \rbrace \rbrace$；滑动关节$J_3$的轴跟$J_4$的轴平行。

图.3: SCARA型机械臂的DH坐标系分配。

图.4: SCARA型机械臂工作区域俯视几何图。

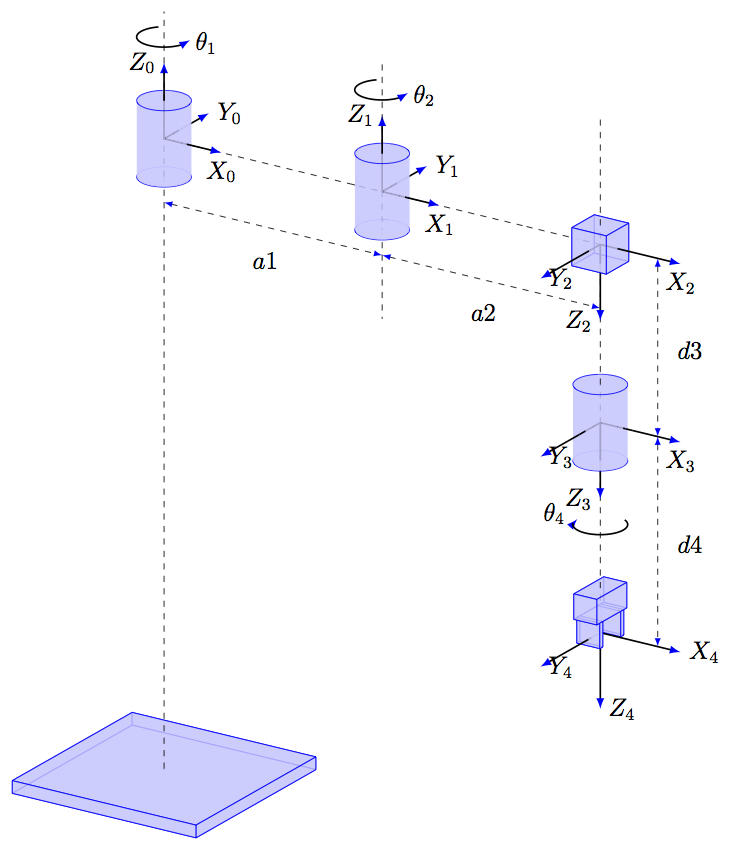
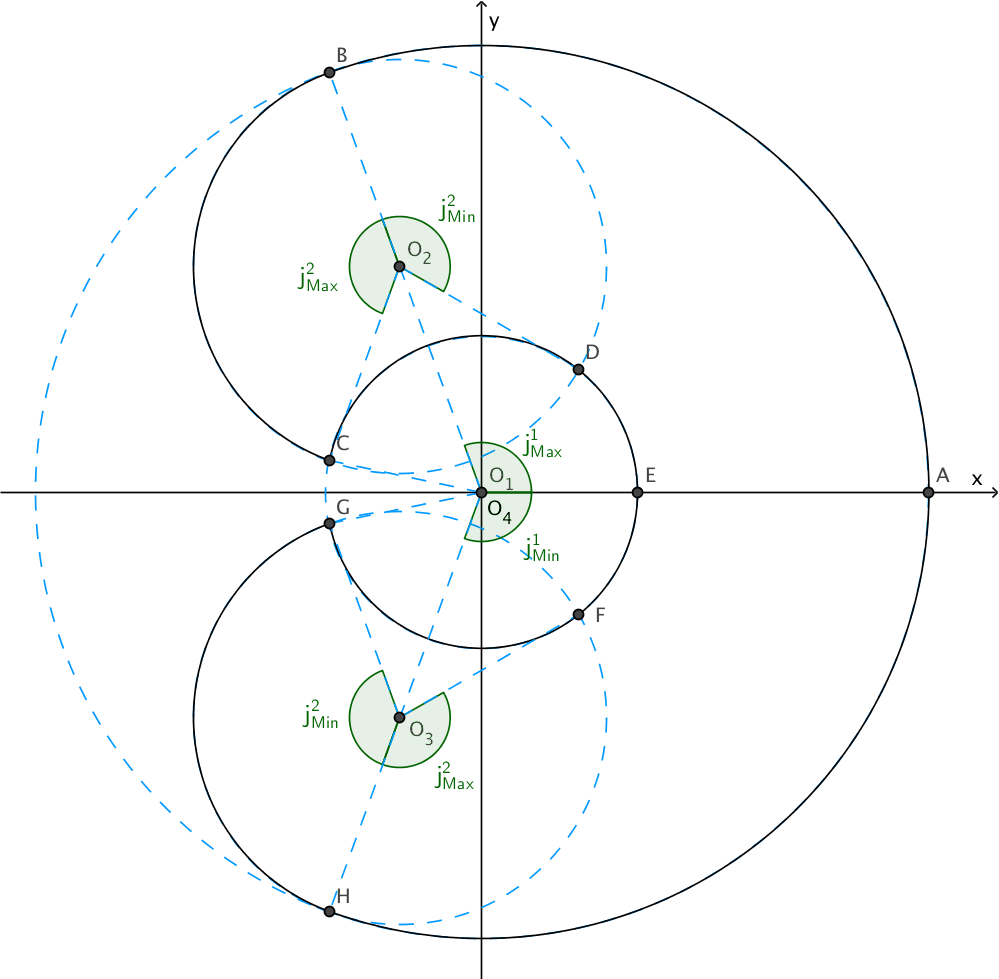
图.3显示了SCARA型机械臂工作区域的俯视几何图。由图可知，机械臂工作区域边界是由$\overparen{HAB}$，$\overparen{BC}$，$\overparen{CEG}$，$\overparen{GH}$四段圆弧所围成的。而圆弧分别位于$\odot{O_1}$，$\odot{O_2}$，$\odot{O_3}$，$\odot{O_4}$四个圆上。圆心$O_1$，$O_4$与$J_1$轴重合；$O_2$和$O_3$分别为$J_1$轴到转动到正负极限时$J_2$轴的位置。$j_{Max}^i$和$j_{Min}^i$分别是电机轴$J_i$的正/负方向的最大活动范围，$j_{Min}^i \le j_{Max}^i$，$\lbrace j^i \mid - \pi \le j^i \le \pi \rbrace$。

由几何关系，我们可以得到：

表.1: 组成工作区域的4个圆弧的几何参数

圆弧	所在圆	圆心$(x_{O_i},y_{O_i})$	半径$r_i$	$\theta _{Min}^i$	$\theta _{Max}^i$
$\overparen{HAB}$	$\odot{O_1}$	${[0,0]}^{^\mathrm{T}}$	$\alpha _1 + \alpha _2$	$j_{Min}^1$	$j_{Max}^1$
$\overparen{BC}$	$\odot{O_2}$	${[\alpha _1\cos(\theta _{Max}^1), \alpha _1\sin(\theta _{Max}^1)]}^{^\mathrm{T}}$	$\alpha _2$	$0$	$j_{Max}^2$
$\overparen{CEG}$	$\odot{O_3}$	${[\alpha _1\cos(\theta _{Min}^1), \alpha _1\sin(\theta _{Min}^1)]}^{^\mathrm{T}}$	$\alpha _2$	$j_{Min}^2$	$0$
$\overparen{GH}$	$\odot{O_4}$	${[0,0]}^{^\mathrm{T}}$	$\left\lvert \overrightarrow {CO_4} \right\rvert$	$\theta _{Min}^4$	$\theta _{Max}^4$

其中： \[\begin{aligned} \overrightarrow {CO_4} &= \left[ {\begin{array}{*{20}{c}} {\alpha _2\cos \theta _{Max}^2\cos \theta _{Max}^1 - \alpha _2\sin \theta _{Max}^2\sin \theta _{Max}^1 + \alpha _1\cos \theta _{Max}^1} \newline {\alpha _2\cos \theta _{Max}^2\sin \theta _{Max}^1 + \alpha _2\sin \theta _{Max}^2\cos \theta _{Max}^1 + \alpha _1\sin \theta _{Max}^1} \end{array}} \right] \newline &= \left[ {f_x}(\theta _{Max}^1,\theta _{Max}^2), {f_y}(\theta _{Max}^1,\theta _{Max}^2) \right]^{^\mathrm{T}} \newline \newline \theta _{Max}^4 &= \arctan({f_y}(\theta _{Max}^1,\theta _{Max}^2), {f_x}(\theta _{Max}^1,\theta _{Max}^2)) \newline \newline \theta _{Min}^4 &= \arctan({f_y}(\theta _{Min}^1,\theta _{Min}^2), {f_x}(\theta _{Min}^1,\theta _{Min}^2)) \end{aligned}\]

假设点$s(x,y)$是圆$\odot{O_i}$边上的一个点，则点$s$相对于圆$\odot{O_i}$的弧度$\theta ^i$为：

\[\begin{equation} \label{SCARA_range_e1} \theta ^i = \begin{cases} \arctan(y, x), & \text{if i=1} \newline \arctan( - x\sin \theta _{Max}^1 + y\cos \theta _{Max}^1,x\cos \theta _{Max}^1 + y\sin \theta _{Max}^1), & \text{if i=2} \newline \arctan( - x\sin \theta _{Min}^1 + y\cos \theta _{Min}^1,x\cos \theta _{Min}^1 + y\sin \theta _{Min}^1), & \text{if i=3} \newline \arctan(y, x), & \text{if i=4} \end{cases} \end{equation}\]

我们假设有射线$R(u)=I+u \cdot \lVert \mathbf{n} \rVert$，起点为$I$，方向向量为$\mathbf{n}$，$\lVert \mathbf{n} \rVert$为方向向量$\mathbf{n}$的单位向量。如果起点在工作区域内，则射线必与某圆$\odot{O_i}$有交点$\kappa _j^{i}$，$\kappa ^i$为射线与圆$\odot{O_i}$的所有交点。$\xi = \lbrace \kappa ^i \rbrace$，$\xi$为所有交点的集合。

图.5显示了其中的一种情况，射线$IP$分别与圆$\odot{O_1}$相交于点$N$；与圆$\odot{O_2}$相交于点$K$和点$M$；与圆$\odot{O_4}$相交于点$J$和点$L$；与圆$\odot{O_3}$没有交点。我们也可以发现，点$K$，$N$虽然在圆上，但是并不在工作区域的弧线上，所以我们在得到交点后，还要查看此时的弧度$\theta ^i$是否满足$\theta _{Min}^i \le \theta ^i \le \theta _{Max}^i$。点$J$为离射线起点最近的有效交点，是我们所寻找的点。

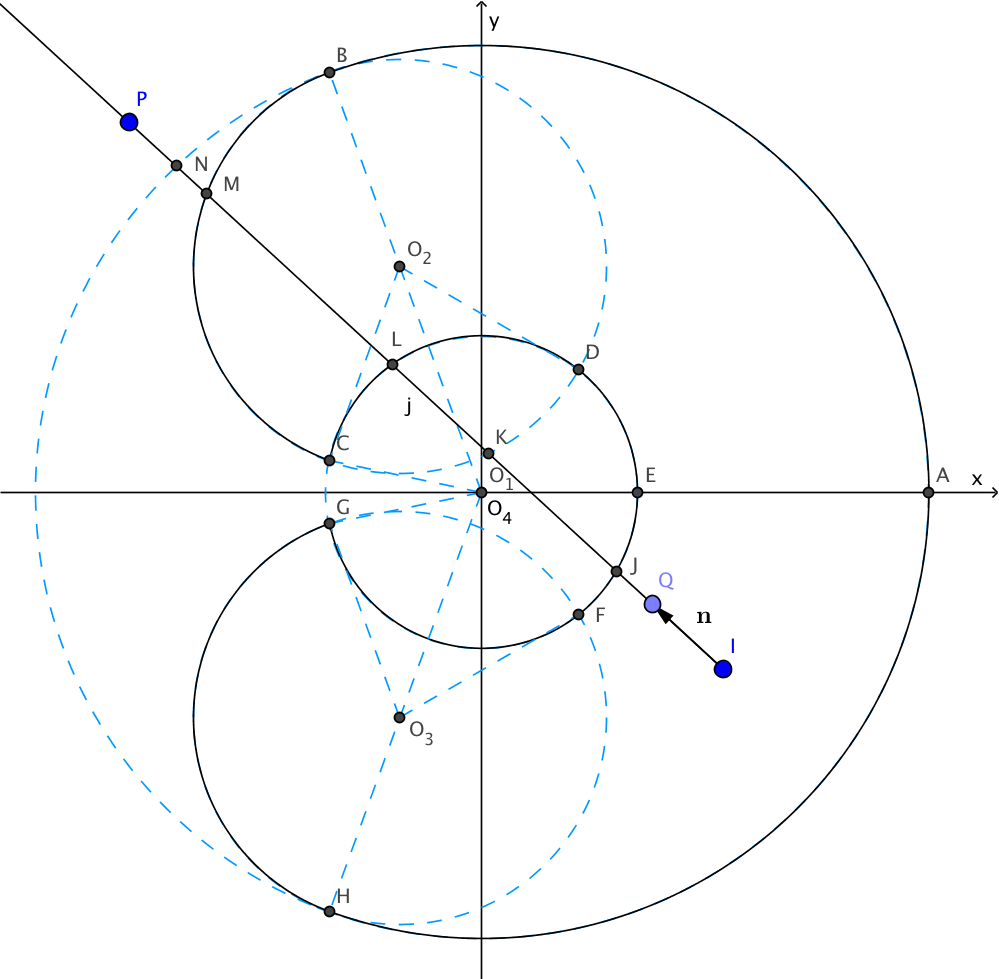Scara_range_report2 图.5: 射线IP与圆$\odot{O_1}$相交于点$N$，$\odot{O_2}$相交于点$M$、$K$，$\odot{O_4}$相交于点$L$、$J$。其中点$J$为射线方向的最近工作区域边缘位置。

算法流程

射线与圆的交点

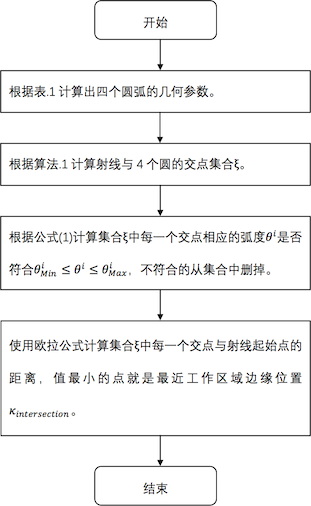
为了确定与给出射线相交的最近的工作区域边缘位置，我们分别计算出射线与每一个圆的交点集$\kappa ^i$。求射线与圆的交点，可以使用传统的参数方程法求交点，另一种方法是使用Akenine-Möller等提出的优化法¹ ²，算法流程如下：

算法.1:Akenine-Möller优化法

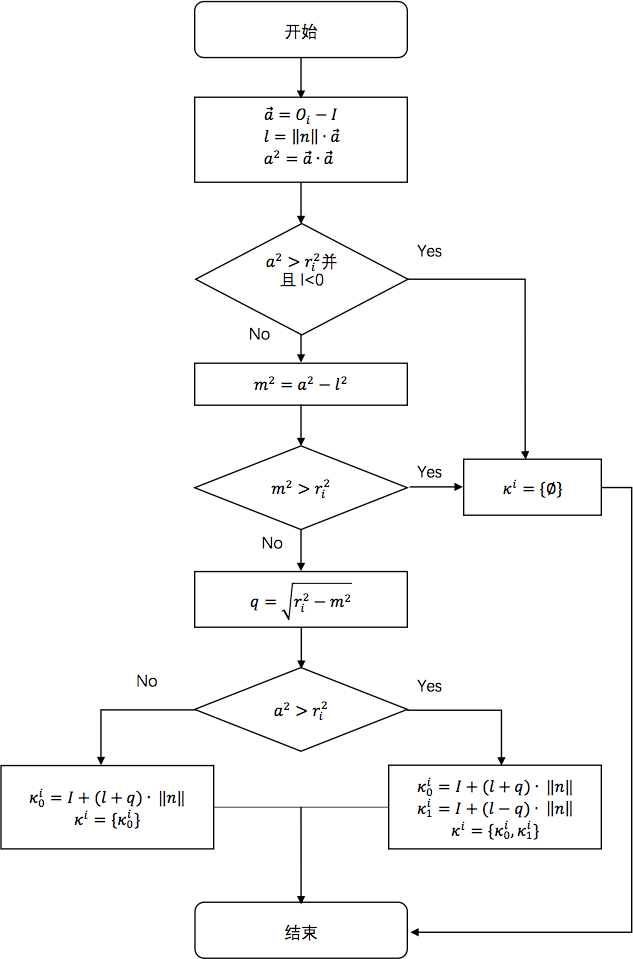
该算法的优点是在计算交点前，先排除掉没有交点的情况，从而减少运算量。

整个算法流程

输入： 1. 射线$R(u)=I+u \cdot \lVert \mathbf{n} \rVert$ 2. 轴$J_1$，$J_2$各自的臂长$\alpha_{1}$，$\alpha_{2}$以及活动范围$ j_{Max}^1 $，$ j_{Min}^1 $，$ j_{Max}^2 $，$ j_{Min}^2 $。

输出： 1. 最近的工作区域边缘位置$\kappa_{intersection}$。

算法.2: 边缘计算流程图

圆弧	所在圆	圆心\((x_{O_i},y_{O_i})\)	半径\(r_i\)	\(\theta _{Min}^i\)	\(\theta _{Max}^i\)
\(\overparen{HAB}\)	\(\odot{O_1}\)	\({[0,0]}^{^\mathrm{T}}\)	\(\alpha _1 + \alpha _2\)	\(j_{Min}^1\)	\(j_{Max}^1\)
\(\overparen{BC}\)	\(\odot{O_2}\)	\({[\alpha _1\cos(\theta _{Max}^1), \alpha _1\sin(\theta _{Max}^1)]}^{^\mathrm{T}}\)	\(\alpha _2\)	\(0\)	\(j_{Max}^2\)
\(\overparen{CEG}\)	\(\odot{O_3}\)	\({[\alpha _1\cos(\theta _{Min}^1), \alpha _1\sin(\theta _{Min}^1)]}^{^\mathrm{T}}\)	\(\alpha _2\)	\(j_{Min}^2\)	\(0\)
\(\overparen{GH}\)	\(\odot{O_4}\)	\({[0,0]}^{^\mathrm{T}}\)	\(\left\lvert \overrightarrow {CO_4} \right\rvert\)	\(\theta _{Min}^4\)	\(\theta _{Max}^4\)