SCARA机械臂三四轴解耦
运动学分析
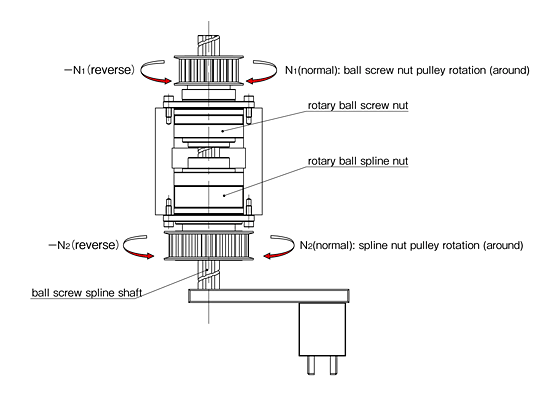
SCARA机械臂3、4关节\(J_3\),\(J_4\)采用滚珠丝杠滚珠花键,其结构如图11所示。关节\(J_3\)与同步轮\(N_2\)联动,关节\(J_4\)与同步轮\(N_1\)联动。他们的运动关系如表1所示。
表. 1:电机与滚珠丝杠滚珠花键运动关系表
| \(\theta_{J_3}\) | \(\theta_{J_4}\) | \(\theta_{N_1}\) | \(\theta_{N_2}\) | 竖直运动 | 旋转运动 |
|---|---|---|---|---|---|
| + | 0 | 0 | + | - | - |
| - | 0 | 0 | - | + | + |
| 0 | + | + | 0 | + | 0 |
| 0 | - | - | 0 | - | 0 |
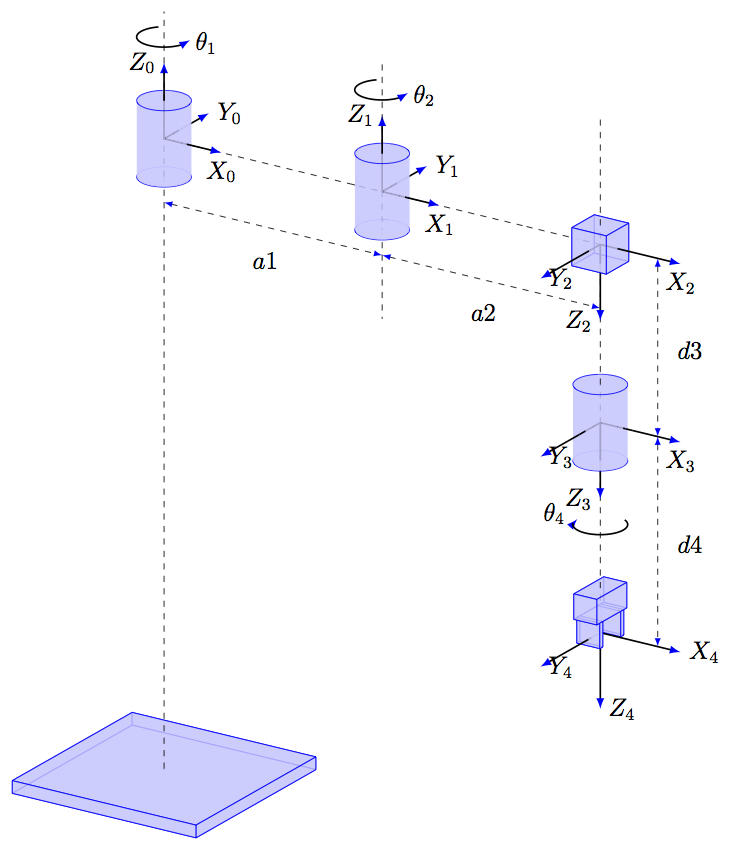
其中,\(+\)号表示正方向,\(-\)表示逆方向,\(0\)表示不运动,要注意\(\theta_{J_3}\),\(\theta_{J_4}\),\(\theta_{N_1}\),\(\theta_{N_2}\)的方向是根据各自所在的坐标下的,具体方向根据图.2所示的DH(Denavit-Hartenberg)坐标系定义,而竖直运动和旋转运动是相对于\(X_0Y_0Z_0\)基坐标系。
从表中可以看出,当关节电机\(J_4\)带动同步轮\(N_1\)进行正方向运动(\(X_3Y_3Z_3\)坐标系),而\(N_2\)不动时,轴仅仅会向上运动(相对于\(X_0Y_0Z_0\)基坐标系)。当关节电机\(J_3\)带动同步轮\(N_2\)进行正方向运动(\(X_2Y_2Z_2\)坐标系),而\(N_1\)不动时,轴在向下运动同时,还会逆时针反方向运动(\(X_0Y_0Z_0\)基坐标系)。由此可见,\(N_1\)和\(N_2\)相互耦合,需要配合运动。在机械人中,通过逆运动学求得\(d_3\),\(\theta_4\)后,需要通过关节解耦求出电机的转角\(\theta_{J_3}\),\(\theta_{J_4}\)2。
关节解耦
经上述分析,可得出以下关系式:
对于\(N_1\),有:
\[\begin{align} {y_1} &= \alpha {\theta _{N_1}} \nonumber \newline {\theta _{N_1}} &= {k_1}{\theta _ {J_4}} \nonumber \newline \therefore {y_1} &= \alpha {k_1}{\theta _{J_4}} \label{eq:jieou1} \end{align}\]
其中,\(y_1\)表示\(N_1\)运动导致的竖直方向位移(\(X_0Y_0Z_0\)坐标系);\(\alpha\)为螺距,单位为\(m/rad\),表示为\(N\)转动的弧度\(\theta_{N}\)与所产生轴上下移动的位移比例;\(k\)表示电机\(J\)与同步轮\(N\)之间的减速比。
同样地,对于\(N_2\),有:
\[\begin{align} {y_2} &= -\alpha {\theta _{N_2}} \notag \newline {\theta _{N_2}} &= {k_2}{\theta _{J_3}} \notag \newline \therefore {y_2} &= -\alpha {k_2}{\theta _{J_3}} \label{eq:jieou2} \end{align}\]
则:
\[\begin{align} \label{eq:jieou3} \theta_4 &= {\theta _{N_2}} \newline \label{eq:jieou4} -{d_3} &= {y_1} + {y_2} \end{align}\]
注意\(d_3\)是相对于\(X_2Y_2Z_2\)坐标系的,而\(y_1\),\(y_2\)是相对于\(X_0Y_0Z_0\)坐标系的,由于\(Z_2\)与\(Z_0\)方向相反,所以\(d_3\)前有一个负号。将公式\(\eqref{eq:jieou1}\),\(\eqref{eq:jieou2}\)代入公式\(\eqref{eq:jieou3}\),\(\eqref{eq:jieou4}\),可得:
\[\begin{align} \label{eq:jieou5} {\theta _{J_3}} &= \frac{\theta_4}{k_2} \newline \label{eq:jieou6} {\theta _{J_4}} &= \frac{1}{k_1}({\theta _4} - \frac{d_3}{\alpha}) \end{align}\]
所以,算法流程如下:
- 使用逆运动学方法,将基于基坐标系(Base Frame)\(X_0Y_0Z_0\)的目标点(包括坐标跟姿态)转换成广义坐标(Generalized Coordinates)下的\(d_3\),\(\theta_4\)。
- 使用公式\(\eqref{eq:jieou5}\),\(\eqref{eq:jieou6}\),关节解耦求出电机的转角\(\theta_{J_3}\),\(\theta_{J_4}\)。
在我们的实体机器人中,\(k_1 = 1\),\(k_2 = 1/7\),\(\alpha = 0.016m/2\pi = 0.002546479089 m/rad\),所以有:
\[\begin{align} \label{eq:jieou7} {\theta _{J_3}} &= 7\theta_4 \newline \label{eq:jieou8} {\theta _{J_4}} &= {\theta _4} - 392.69908177d_3 \end{align}\]