自然语言处理
沃森(Watson)
Ibm公司的沃森是能够使用自然语言来回答问题的人工智能系统,它是一个集高级自然语言处理、信息检索、知识表示、自动推理、机器学习等开放式问答技术的应用,并且是基于为假设认知和大规模的证据搜集、分析、评价而开发的DeepQA技术。沃森的基本工作原则是解析线索中的关键字同时寻找相关术语作为回应,信息来源包括百科全书、字典、词典、新闻和文学作品。 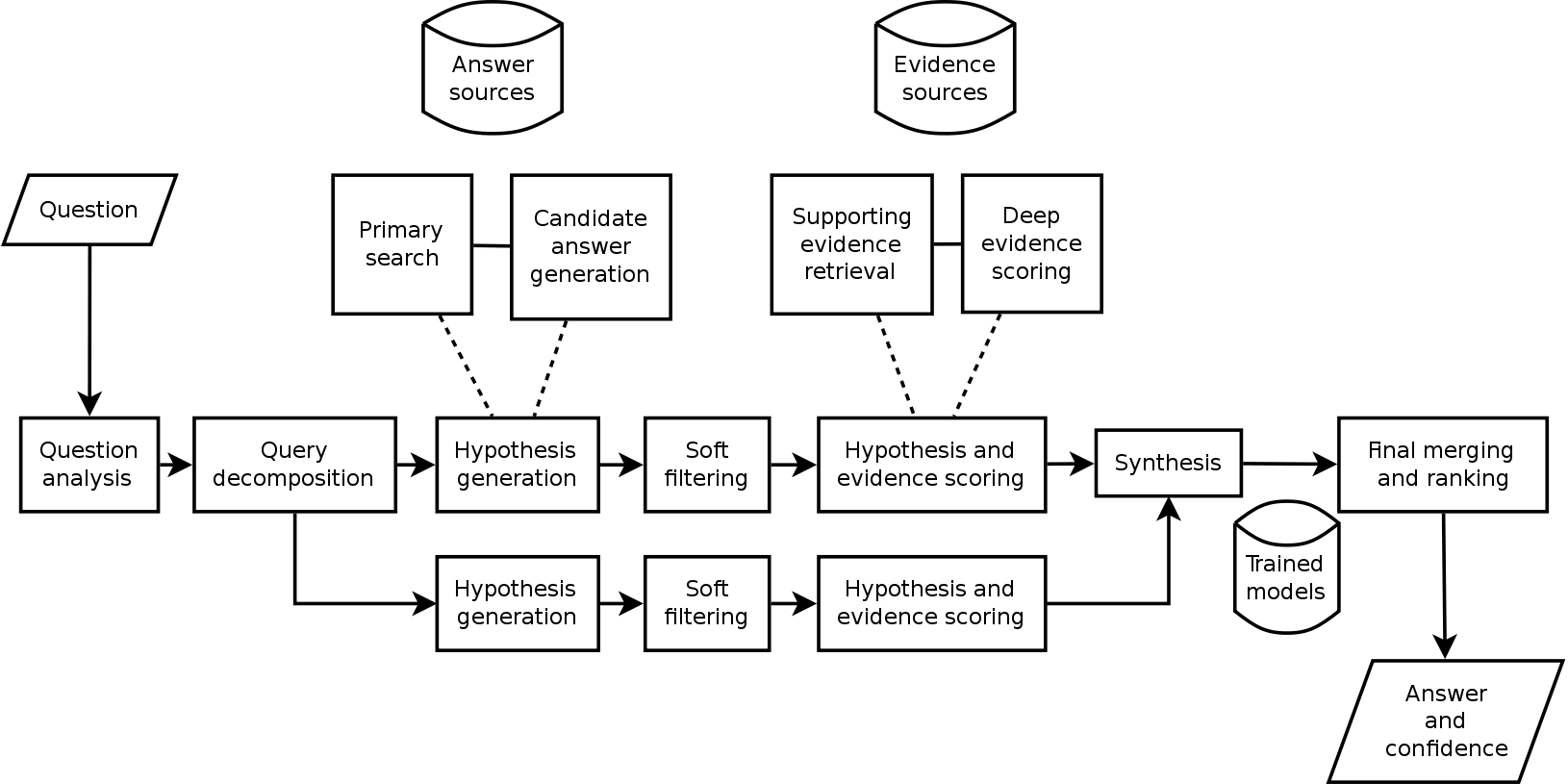 沃森最革新的并不是在于全新的操作算法,而是能够快速同时运行上千的证明语言分析算法来寻找正确的答案。算法找出的相同答案越多,沃森就越肯定答案正确。一旦沃森发现一个潜在的解决方法,并且这个解决方法有效,它就会核对数据库来确定答案。但对于线索较少的问题,沃森表现比不上人类。
沃森最革新的并不是在于全新的操作算法,而是能够快速同时运行上千的证明语言分析算法来寻找正确的答案。算法找出的相同答案越多,沃森就越肯定答案正确。一旦沃森发现一个潜在的解决方法,并且这个解决方法有效,它就会核对数据库来确定答案。但对于线索较少的问题,沃森表现比不上人类。
在2011年,沃森参加综艺节目《危险边缘》,打败了最高奖金得主布拉德·鲁特尔和连胜纪录保持者肯·詹宁斯。之后,沃森首先在医疗领域发力。2015年五月,IBM与美国和加拿大的多家肿瘤中心合作,用沃森系统,根据患者的肿瘤基因选择适当的治疗方案。另外,IBM还与在线心理治疗公司Talkspace合作,沃森系统基于后者人工生成的心理医生匹配数据,帮助医生给出最佳治疗方案。2015年八月,IBM宣布以10亿美元收购医疗影像公司Merge
Healthcare。另外IBM还与美国第二大连锁药店CVS合作,使用沃森系统通过分析相关指标和用户行为,来预测其健康状况。2015年十二月,与诺和诺德合作,希望为糖尿患者开发出“虚拟医生”,为患者提供胰岛素用量等治疗建议。
除医疗领域外,沃森还为音乐公司Ampsy发现和记录实时活动中所有分享和发布社交内容的人。例如,通过沃森驱动分析粉丝对音乐会各个部分喜好度的发布率的数据,能识别出那些“超级粉丝”;为石油公司Woodside提供公关服务,它实时分析和预测网络上可能出现的负面消息,为公关人员提供更具有回击力量的词语和句式;与酒店运营商希尔顿合作,在旗下美国连锁酒店测试一种礼宾机器人。住客可向其提问一些问题,如周边餐厅、旅游名胜和酒店信息等。

图像识别
Google深度学习系统TensorFlow
机器学习作为人工智能的一种类型,可以让软件根据大量的数据来对未来的情况进行阐述或预判。如今,领先的科技巨头无不在机器学习下予以极大投入包括Google,Facebook、苹果、微软,百度。TensorFlo是
Google 多年以来内部的机器学习系统。如今,Google
正在将此系统成为开源系统。TensorFlow 表达了高层次的机器学习计算,大幅简化了第一代系统,并且具备更好的灵活性和可延展性。TensorFlow一大亮点是支持异构设备分布式计算,它能够在各个平台上自动运行模型,从电话、单个CPU / GPU到成百上千GPU卡组成的分布式系统。
统TensorFlow在很多地方可以应用,如语音识别,自然语言理解,计算机视觉,广告等等。但主要还是用在图像识别的领域,并且实现了多种应用:
图片识别
ImageNet是一个包含有100万张图片的测试库,是计算机视觉领域最大的。图片中包含1000种不同分类,每一类有1000张图片。比如里面有上千张不同的豹子,摩托车等,一个麻烦的是不是所有的标签都是对的。

在神经网络使用之前,最好的错误记录是26%,2014年
Google错误率暴降到6.66%取得冠军,然后到了2015年错误率下降到3.46%。而人类的错误率有5.1%。
但是系统也会犯一些比较低级的错误,比如将鼻涕虫识别成蛇:

Google图片搜索
根据对图片内容的识别,自动为图片打标签,方便用户搜索图片。 
看图说话
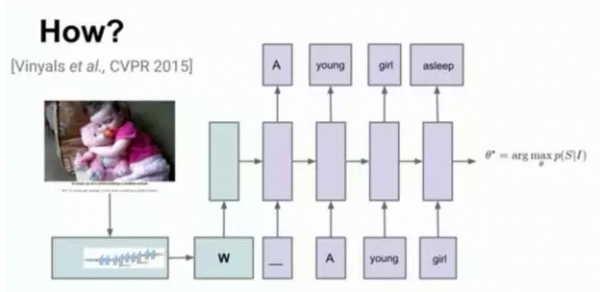
结合图片识别系统,将图片作为输入,输出为文字的描述。训练集有5个由不同的人写的不同的字幕。总共100万图片,70万条语句。效果如下:

不过也有识别错误的时候,比如下图中将飞在空中的风筝识别错了: 
语音技术
语音技术实现了人机语音交互,使人与机器之间沟通变得像人与人沟通一样简单。语音技术主要包括语音合成和语音识别两项关键技术。让机器说话,用的是语音合成技术;让机器听懂人说话,用的是语音识别技术。此外,语音技术还包括语音编码、音色转换、口语评测、语音消噪和增强等技术。
语音合成
机器人声合成的原理就是将基础音从样本中解析出来,并且重新组合成目标语言。概括说,这个过程一般包括(假设是较为复杂的跨语言语音助手,同语言的会更简单些):
1. 解析英语文本:分析出英文语义,并且解析出人声基础音 2.
将英文语义转化成中文语义 3. 分析构建中文语义所需的基础音 4.
利用用户已有的基础音构建相应的中文发声(如果所需要的基础音缺乏,则去云端进行匹配搜索,寻找相近的基础音进行替换,这里需要用到事先的人声配音)
5.
根据情感分析结果,对中文发声序列进行调整,从而更加符合语调和情感。
其中做得比较好的是微软的Cortana。它能理解用户的话外之音,寻找探测声调里表示情感的基本元素,能让Cortana听起来更自然。而且Cortana能够将犹豫、停顿、呼吸、咳嗽和其它一些非词汇的发音放到该放的地方,让语音听起来更加自然。
语音识别
语音识别技术中,国际厂商主要以Nuance、Google、微软、apple为主;国内则有科大讯飞、飞捷通华声、百度、搜狗、腾讯等厂商。
因为高质量的语音识别确实需要大量的存储空间和计算能力,所以目前市面上的应用一般都采取语音上传,服务器端分析的方式。所以对于网络有一定的要求。
在众多的产品中,苹果的Siri的优势在于和iOS整个生态系统(特别是原生应用)的整合性强,功能点多。劣势在于其识别的精度相比于业界目前相对完善的Google
Now较低。Google
Now已经能够非常好的根据上下文对用户的输入进行自动修正,从而构建有效的问答。但是Siri还无法很好地做到。
语音技术十分依重与基础的数据源,但国内的基础资源市场现状仍不容乐观,还有大量的空白需要填补。目前的现状是:数据种类少,分布不均匀,尤其是方言、重口音、外语类资源仍然特别短缺;中小型、适合学术和科研使用的数据虽多但质量较差,大规模、高质量工程化数据资源还是比较稀缺;数据的重复开发情况比较普遍,但重复利用度低,缺乏数据共享机制。
神经工程系统
今年,美国国防部高级研究计划局(
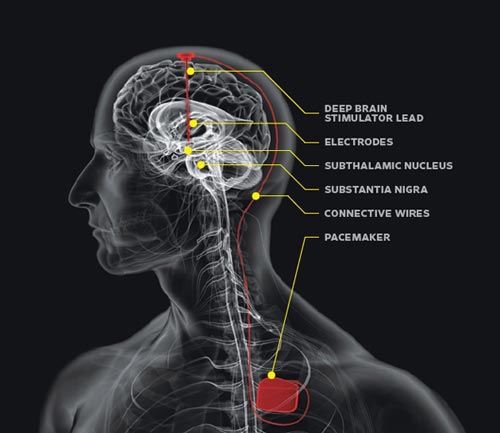
DARPA)启动了一个新项目,计划开发人脑和计算机之间的界面。通过这样的界面,人脑可以直接控制计算机,而用户将不必再动手操作。他们计划将大小不超过1立方厘米的“生物兼容设备”植入到大脑中,将人脑使用的生物化学语言转换成计算机信号。该项目的重点在于脑部植入的芯片,而比较出名的有Medtronic开发了deep
brain simulation(DBS)。
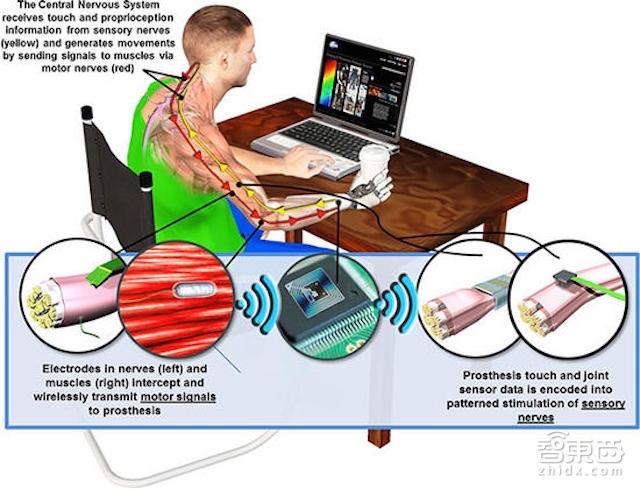
而在这之前,DARPA与2015年已经对外宣布已经成功研制出带有触觉的机械义肢。此机械义肢项目需要攻克的技术难点在于放大脑对于“脑——手”神经系统的控制信号,具体来说,传入神经信号由是指压力传感扭矩马达传出,他们希望义肢的手感受任何到触摸感觉时,大脑能传达出一种像肉与骨头相触的电信号。
即使这个硬件概念已经做成实物,但DARPA方面仍有许多工作需要完善。比如,该义肢的压力传感器并没有覆盖整只手,也没有考虑到温度等其它环境条件等。
群体机器人
当我们需要的任务繁重复杂时,单个机器人有可能会遇到困难,这时则需要多机器人协同完成任务。
Kiva
仓库搬运工作是一项繁重的体力活。业内人士称,仓库工人60%-70%的时间花费在取货上。而亚马逊的Kiva机器人系统,能精确地识别出需要搬走的货架,然后钻到货架底下,干净利落地“扛起来”,搬到工人旁边,再由工人取下货物,包装、发走。
机器人拥有多个摄像头,朝上的摄像头读取二维码,这些二维码能够识别独一无二的货架,并实现货架的接驳。朝下的摄像头处理坐标点信息,以确定机器人的位置。作为核心的Kiva
MFS管理系统能够对3000台机器人进行任务规划,跟踪。

 沃森最革新的并不是在于全新的操作算法,而是能够快速同时运行上千的证明语言分析算法来寻找正确的答案。算法找出的相同答案越多,沃森就越肯定答案正确。一旦沃森发现一个潜在的解决方法,并且这个解决方法有效,它就会核对数据库来确定答案。但对于线索较少的问题,沃森表现比不上人类。
沃森最革新的并不是在于全新的操作算法,而是能够快速同时运行上千的证明语言分析算法来寻找正确的答案。算法找出的相同答案越多,沃森就越肯定答案正确。一旦沃森发现一个潜在的解决方法,并且这个解决方法有效,它就会核对数据库来确定答案。但对于线索较少的问题,沃森表现比不上人类。








